Week 10: El Ni~no Southern Oscillation

The El Niño-Southern Oscillation (ENSO) represents one of the most significant sources of variability on seasonal to interannual timescales. Its global influence spans multiple domains, impacting phenomena like spring tornado frequency in the continental US, variability in the North Western subtropical high, tropical cyclone activity, and patterns of global warming. These examples are just the tip of the iceberg. ENSO typically cycles every 2–7 years, making it highly predictable on seasonal scales. Its profound global impacts and predictability have made modeling ENSO one of the climate science community’s enduring challenges.

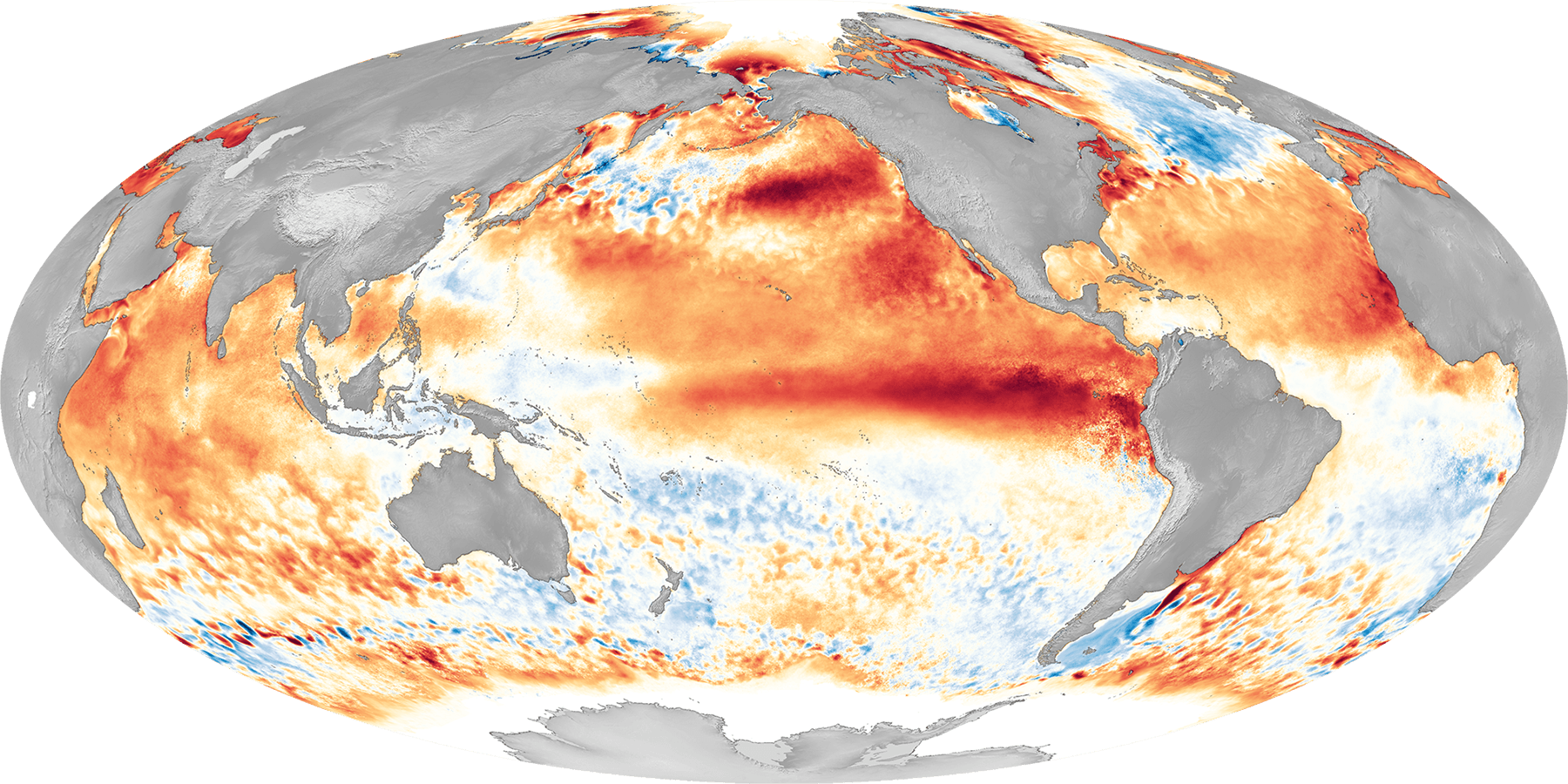
Fig. 29 The 2016 El Niño event. Credit: NOAA_PSL.

Background

The earliest recorded observation of ENSO dates back to 1892 when a sailor in Peru noted its effects, long before its theoretical foundation was established. In 1969, [Bje69] introduced a conceptual model describing the positive feedback mechanisms in tropical air-sea interactions. ENSO theory was further developed when Drs. Mark Cane and Stephen Zebiak proposed a modeling framework integrating (1) the atmosphere, (2) the ocean’s mixed layer, and (3) thermocline dynamics. Building on their prototype, two major theories emerged to explain ENSO variability: (1) Wave Theory and (2) the Recharge-Discharge Mechanism. Among wave theories, the Delayed Oscillator model, advanced by Drs. Max Suarez, Paul Schopf, David Battisti, and Anthony Hirst, is particularly notable. The recharge-discharge oscillator was proposed by Dr. Fei-Fei Jin, with further contributions by Dr. Tim Li.

Warm Water Volume (Recharge-Discharge Mechanism)

We will explore key processes underlying ENSO. Both the recharge-discharge mechanism and the delayed oscillator are simplified interpretations of the more complex Zebiak and Cane models, enabling better physical insights.

The recharge-discharge mechanism is summarized in the diagram below:

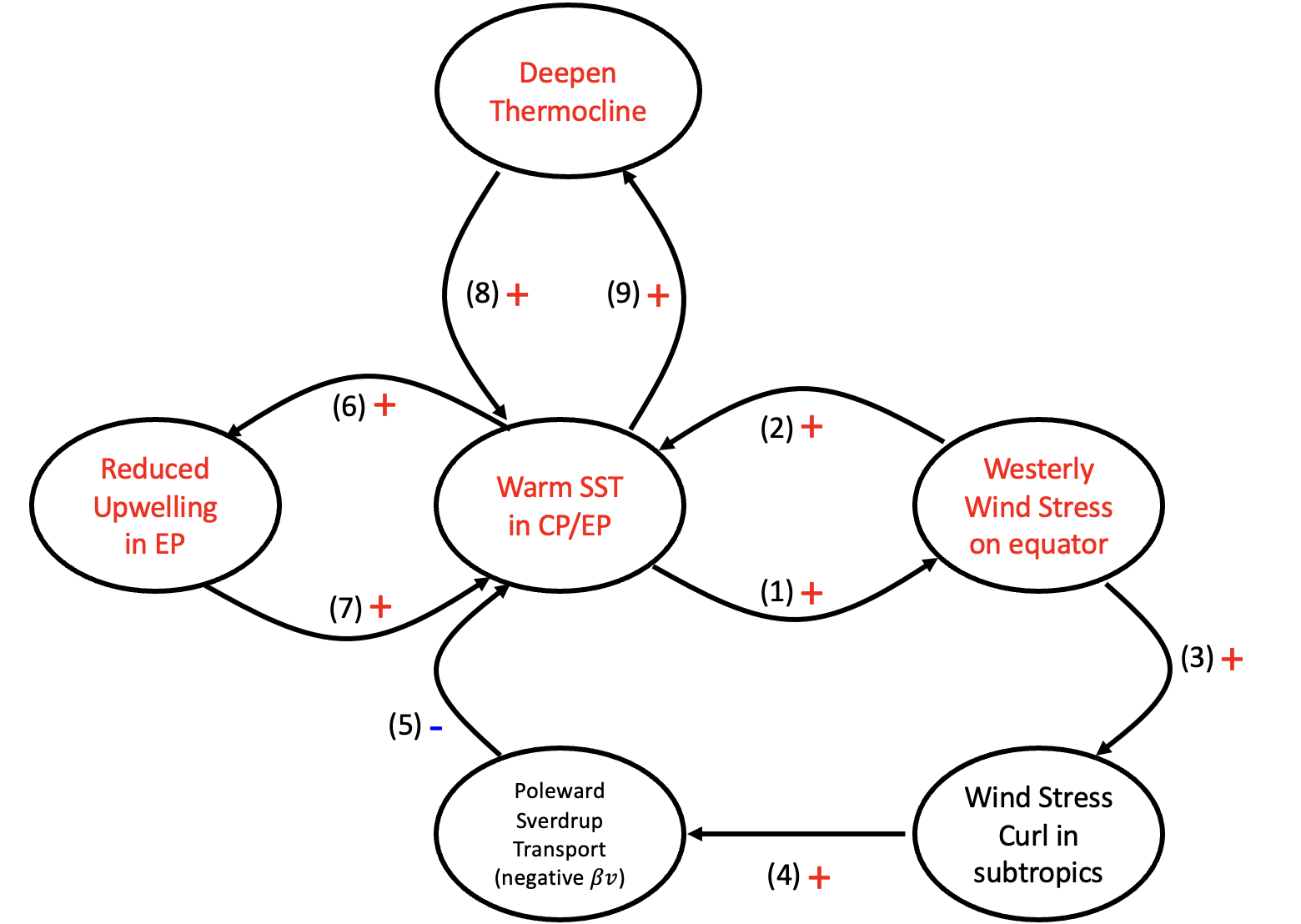
Fig. 30 The (known) feedback processes in ENSO.

Key Processes: (1)+(2) Bjerknes Feedback: Warm sea surface temperatures (SSTs) in the central/eastern Pacific weaken the Walker Circulation, favoring convection in these regions. Enhanced westerly winds transfer warm water eastward.

(3)+(4)+(5) Subtropical Feedback: Westerly winds increase cyclonic wind stress curl in subtropical areas. To balance reduced relative vorticity, poleward geostrophic currents transport warm water to higher latitudes and shallow the equatorial thermocline. The opposite occurs during La Niña.

(6)+(7) Ekman Feedback: Westerly winds during El Niño years suppress equatorial upwelling through Ekman pumping.

(8)+(9) Thermocline Feedback: A deepened thermocline reduces the ability of upwelling to bring cooler subsurface water to the surface.

These processes collectively form the recharge-discharge oscillator described by [Jin97]. Oscillations require at least one negative feedback, and SST and thermocline depth are primary predictors, with atmospheric processes modeled as steady states due to their transient nature compared to ocean processes.

Note

Sverdrup balance was first used to explain the existence of Western Boundary current. It was then modified by Dr. Biran Hoskins to explain the extension of subtropical high and monsoon gyre. (See Hoskins and Rodwell). Dr. Fei-Fei Jin was working with Dr. Brian Hoskins

(91)\[\begin{split}\begin{align} \frac{dT}{dt}=CT+Dh-\epsilon T^3 \\ \frac{dh}{dt}=-ET-R_h \end{align}\end{split}\]

Details of each term will be provided in the final project.

Wave School (the oscillators)

Delayed oscillator

Fig. 31 The simulated ENSO evolution is based on McCreary model.

McCreary hypothesized that the reflection of oceanic Rossby waves can help generate the interannual variability of SST. By emphasizing on the western boundary, Suarez and Schopf (1988) proposed the prototype of the delayed oscillator. Zebiak and Cane then coupled an atmospheric Gill model with a 1.5-layer SST model (mixed layer + thermocline dynamics) becoming the first who successfully predicted the ENSO. [BH89] used such an intermediate model to propose the well-know delayed oscillator mechanism.

Different from the Recharge-discharge oscillator, the delayed oscillator focuses on the transient dynamics and explains the change of warm water volume and SST through a wave lens.

The delayed oscillator can be formulated as follows:

(93)\[\begin{align} \frac{dT}{dt} = AT-BT(t-\eta)-\epsilon T^3 \end{align}\]

where T represents the SST anomaly in the equatorial eastern Pacific. The first term on the right-hand side is the Bjerknes feedback between the ocean and the atmosphere. The second term represents the negative feedback due to the wave reflection on the western boundary. The cubic term is a higher-order damping (doesn’t rule out the periodicity). Overall, the Delayed oscillator focuses on the western boundary processes but can capture most of the variability found in the Zebiak and Cane model.

Western-Pacific Oscillator

Weisberg and Wang (1997) expanded on the delayed oscillator, emphasizing the role of western Pacific dynamics. This oscillator captures the interplay of equatorial westerlies, upwelling, and cyclones using more detailed formulations:

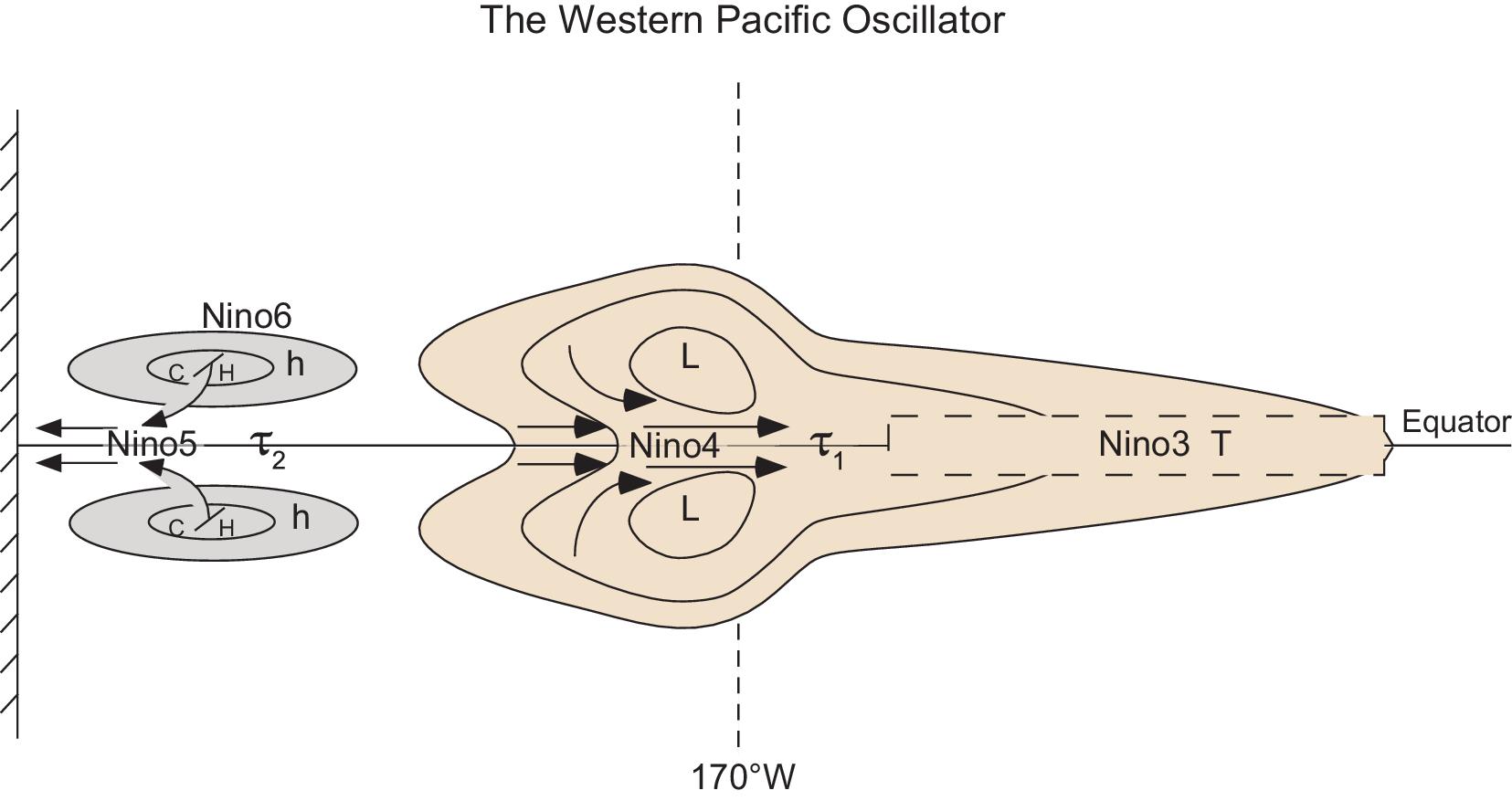
Fig. 32 The western Pacific oscillator in the Delayed oscillator. From Wang (2018): A review of ENSO theories.

and the corresponding equation

(93)\[\begin{split}\begin{align} \frac{dT}{dt} &= a \tau_1 +b_2\tau_2(t-\delta)-\epsilon T^3 \\ \frac{dh}{dt} &= -c \tau_1(t-\lambda)-R_hh \\ \frac{d \tau_1}{dt} &= dT -R_{\tau_1}\tau_1 \\ \frac{d \tau_2}{dt} &= eh -R_{\tau_2}\tau_2 \\ \end{align}\end{split}\]

Where, T, h, \(\tau_1\) and \(\tau_2\) are illustrated in Fig. 32

We first start with equatorial westerly. The equatorial westerly (\(\tau_1\)) at Nino 4 driven by tropical convection (like MJO) will drive a downwelling Kelvin wave (warm anomaly) which further propagates eastward to increase Nino 3 temperature. This is represented in the first term of equation 1. At the same time, the atmospheric Gill response also drives twin cyclones off the equator. The twin cyclone can induce oceanic upwelling due to Ekman pumping, which further expands westward to the Nino 6 regions (as indicated in the time-delayed term of \(\tau_1(t-\lambda)\)). The cold SST then triggers surface high, which induces equatorial easterly at Nino 5. Unlike the equatorial westerly, the equatorial easterly will induce upwelling Kelvin wave, reversing the warm anomaly pattern. Such equatorial easterly has been the main focus over the past few years (i.e., Dr. Wayne Lee’s PhD work).

Advective-reflective oscillator

The advective-reflective oscillator is very similar to the previous two oscillators except looking into the wave reflection on both sides of the basin.

The Primitive Equation-based ENSO models

While these oscillators/theories focus on different aspects of ENSO, they all got some success in simulating ENSO due to the strong air-sea coupling, i.e., omitting one or a few variables won’t hurt the main variability as long as the omitted variables can be represented by other processes.

For a more completed picture, the [McC83] and [ZC87] models have incorporated all of the ingredients above using the primitive equations. Both models are a combination of (1) one oceanic shallow water model and (2) a diagnostic atmosphere component. Here we use McCreary Model as an example.

For the oceanic component,

(94)\[\begin{split}\begin{align} & u_t -\beta y v + p_x = F + \nu_h \nabla^2 u \\ & v_t +\beta y u + p_y = G + \nu_h \nabla^2 v \\ & p_t + c^2 (u_x+v_x) = 0 \end{align}\end{split}\]

The ocean model (94) is nearly identical to the atmospheric Gill model. The only difference is the existence of wind stress forcing (i.e., \(F\) and \(G\), which are \(\tau_x/H\) and \(\tau_y/H\) respectively). The wind stress forcing is the main process in triggering the oceanic waves.

(95)\[\begin{split}\begin{cases} \tau_h &= \tau_{0h}X(x-x_h)Y_h(y) \\ \tau_w &= \tau_{0w}X(x-x_w)Y_w(y) \\ \tau_b &= \tau_{0b}X(x-x_b)Y_b(y) \\ \end{cases}\end{split}\]

(96)\[\begin{split}\begin{align} X(x) & = \mathrm{cos} (2\pi x/D) \\ Y_h(y) & = 1/2[1-\mathrm{cos} (2\pi y/\lambda_h)] \\ Y_w(y) & = 1/2[1+\mathrm{cos} (2\pi y/\lambda)] \\ Y_b(y) & = 1/2[1-\mathrm{cos} (2\pi y/\lambda)] \end{align} \begin{cases} |x|\leq D/4 \\ |y|\leq \lambda_h \\ |y|\leq \lambda/2 \\ |y|\leq \lambda \\ X = Y_h = Y_w = Y_b = 0, \text{otherwise} \end{cases}\end{split}\]

where \(x_h\) = 7500km, and \(x_w\) = \(x_b\) = 5000km. \(\tau_{0h}\) = -0.025\(N\cdot m^{-1}\), and \(\tau_{0w}\)=\(\tau_{0b}\) = -0.05\(N\cdot m^{-1}\). \(D\) is the zoanl domain size. The structure of \(\tau_b\) and \(\tau_h\) are the same except \(\tau_{b}\) is located in the central Pacific and \(\tau{h}\) is located in the eastern Pacific. \(\tau_h\) represents enhanced Hadley cell and enhanced trade wind centered off equator. \(\tau_{w}\) represents an enhanced equatorial esterly or well-developed Walker cell.

The model wind stress forcing is only witched between two states (1) enhanced off-equator trades at the eastern Pacific and (2) enhanced trades at the equator, where the switch is eastern boundary SST. u.e.,

(97)\[\begin{split}\tau_x = \begin{cases} \tau_b +\tau_h \text{ when $h_e>h_c$} \\ \tau_b +\tau_w \text{ when $h_e\leq h_c$} \\ \end{cases}\end{split}\]

when eastern Pacific is anomalously warm, we have reduced equatorial trades but enhanced subtropical trades and vice versa. With such simple setup, climate scientists are able to simulate interannual variability similar to the observed ENSO.

Fig. 31 shows the simulations with modified parameters (with \(x_w\) = \(x_b\) = 3000km and \(x_h\) = 5000km and keep the rest the same). One can find the equatorial westerly can trigger off-equatorial downwelling Rossby waves that propagate westward and reflect as an equaotiral Kelvin wave (downwelling) at the western boundary. When the reflected waves touch the eastern boundary, it change the intensity of Walker circulation and thus change the equatorial trades intensity.

On the other hand, one can also find the Recharge-discharge mechanisms in the simulation. When the eastern Pacific is anomalously warm/cold (and during its peak phase), the difference in warm water volume over the western Pacific is small (during its peak transition). On the contrary, when the eastern Pacific has small change in SST, the difference in warm water volume between the subtropics and the tropics is the largest.

The Recharge-discharge oscillator describes evolution in eastern Pacific SST and western Pacific warm water volume. These two variables are orthogonal in time and thus their interaction forms an oscillation.

ENSO Diversity

More recently, the scientific community found that ENSO is characterized by different behaviors after 2000. Speficically, the anomalously warm SST is shifted toward central Pacific (CP ENSO) rather than centered around eastern Pacific (EP ENSO). Such shift in ENSO regimes is also found can ba captured through idealized model indicating that the fundamental processes have been incoorporated in those models.

The shifted of SST center has important global implication. First, it changes the life-cycle of ENSO. The CP ENSO has generally shorter life cycle than its EP counterpart. Second, the teleconnection generated by ENSO is more sensitive to the SST change in central Pacific than the Eastern Pacific. One reason is that the interaction between ENSO-induced tropical divergent wind has stronger interaction with Western Pacific subtropical jet. Thus, even CP ENSO is usually characterized by weaker amplitude, its global impacts are no less than EP ENSO.

AK16

Á F Adames and D Kim. The MJO as a dispersive, convectively coupled moisture wave: theory and observations. J. Atmos. Sci., 2016.

AW15

Ángel F Adames and John M Wallace. Three-dimensional structure and evolution of the moisture field in the MJO. J. Atmos. Sci., 72(10):3733–3754, October 2015.

BH89

David S Battisti and Anthony C Hirst. Interannual variability in a tropical atmosphere–ocean model: influence of the basic state, ocean geometry and nonlinearity. J. Atmos. Sci., 46(12):1687–1712, June 1989.

Bje69

J Bjerknes. Atmospheric teleconnections from the equatorial pacific1. Mon. Weather Rev., 97(3):163–172, March 1969.

HL72

James R Holton and Richard S Lindzen. An updated theory for the quasi-biennial cycle of the tropical stratosphere. J. Atmos. Sci., 29(6):1076–1080, September 1972.

Jin97

Fei-Fei Jin. An equatorial ocean recharge paradigm for ENSO. part I: conceptual model. J. Atmos. Sci., 54(7):811–829, April 1997.

LNK+22

Yi-Xian Li, J David Neelin, Yi-Hung Kuo, Huang-Hsiung Hsu, and Jia-Yuh Yu. How close are leading tropical tropospheric temperature perturbations to those under convective quasi equilibrium? J. Atmos. Sci., 79(9):2307–2321, September 2022.

LH68

Richard S Lindzen and James R Holton. A theory of the quasi-biennial oscillation. J. Atmos. Sci., 25(6):1095–1107, November 1968.

MJ71

Roland A Madden and Paul R Julian. Detection of a 40-50 day oscillation in the zonal wind in the tropical pacific. Journal of Atmospheric Sciences, 28:702–708, July 1971.

Mat66

Taroh Matsuno. Quasi-geostrophic motions in the equatorial area. J. Meteorol. Soc. Japan, 44(1):25–43, 1966.

McC83

Julian P McCreary, Jr. A model of tropical ocean-atmosphere interaction. Mon. Weather Rev., 111(2):370–387, February 1983.

RH96

Mark J Rodwell and Brian J Hoskins. Monsoons and the dynamics of deserts. Quart. J. Roy. Meteor. Soc., 122(534):1385–1404, July 1996.

ZC87

Stephen E Zebiak and Mark A Cane. A model el niñ–southern oscillation. Mon. Weather Rev., 115(10):2262–2278, October 1987.