Week 3: The minimalist models for studying chaos and predictability I: Lorenz 63¶

In weeks 1 and 2, we learned how to define predictability and explore the potential predictability sources in Earth atmosphere. This week, we will talk about the origins of the studies of predictability and chaos.

Next to relativity and statistical mechanics, chaos is probably one of the most groundbreaking discoveries in theoretical physics in 20th century. Although Edward Lorenz is not “the” father of chaos theory (some fundamental work had been done by Henri Poincare), he was definitely one of a few pioneers who systematically unraveled this field. This week, we will walk through the details of his legendary 63 paper: “Deterministic non-periodic flow”[Lor63].

The origins of the story¶

Some of you might have heard of the story that Edward Lorenz (Ed hereafter) accidentally found “chaos” when he was dealing with the rounding error problem. Specifically, when he tried to save the simulation output for the next experiments (while he was taking a break for a cup of coffee), he unpurposefully truncated the data which led a totally different simulated result at the end. He then realized that for a non-linear chaotic system, even an infinite error in the initial state can ultimately lead to an unpredictable future i.e., the relation between aperiodicity and the loss of prediction skills.

To better understand how the small initial error led to an chaotic future, Ed needed a system, which was both chaotic but also simple enough for understanding (also see this workshop in honor of Lorenz and Charney). At the very beginning, Ed was working on a set of equation with 12 variables mimicking the state-of-art forecast system

(16)¶\[\begin{align*} \frac{dX_i}{dt}=\sum_{m,n}a_{imn}X_mX_n+\sum_{m}b_{im}X_m+c \end{align*}\]

With the chosen parameters, he found some non-periodic behaviors for this set of equations. However, it was too complicated to boil down (and later in his career, he found it’s impossible to simplify this equation). So…Ed continued searching for a much simpler system. His effort bore fruits when he visited Barry Saltzman in 1961 [Sal62]. Barry showed him 7 equations representing the convective system, where most of them showed periodic behavior except one refused to settle down. This was the famous Rayleigh-Bernard convection[Ray16], also the starting point of the famous Lorenz 63 model.

Note

Equation (16) is so-called Lorenz 96 model[Lor96], which describes non-linear waves propagating in a single zonal band. More details will be provided next week. One reason making it impossible to simplify is that when we try to solve the linearnized (16) (stability test, see week 7), it will lead a polynomial equation with orders higher than 5 (i.e., \(\sum_{n=1}^{N} a_n x^n\) where N\(\geq 5\). According to Galois theory, there is no analytical solution for a polynomial equation with order higher than 5 (or can’t be represented with the existing math symbols such as +,-, X, / or \(()^{\frac{1}{n}}\) (\(\forall n\in N\)) without introducing the concept of infinity).

Rayleigh-Barnard Convection¶

Rayleigh-Barnard problem is a set of equation describing the convective-driven/diffusion-driven flow. Obviously, there are two competing forces of mass transport in this kind of flow (1) buoyancy and (2) drag. So we need momentum and thermodynamics equations in Rayleigh-Barnard problem.

(17)¶\[\begin{split}\begin{align*} \frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot\nabla)\mathbf{u} &=\nu\Delta\mathbf{u}-\frac{\nabla_h p}{\rho_0}+(\alpha T)g \\ \frac{\partial T}{\partial t}-u_z\Gamma+ (\mathbf{u}\cdot\nabla_h)T &=\kappa\Delta T \\ \nabla\cdot \mathbf{u} &= 0 \end{align*}\end{split}\]

where \(\mathbf{u}\) is 3-dimensional momentum in vector form, g is the gravitational acceleration, T is the departure of temperature from a reference temperature profile (or potential temperature since we will introduce Boussinesq approximation later). \(\alpha\) is the coefficient of thermal expansion (not specific volume), which is define as \(\frac{1}{A}\frac{dA}{dT}\) (A is volume and T is the temperature). The last term in first equation of (17) is so-called reduced gravity or buoyancy. \(u_z\) is the vertical velocity and \(\Gamma\) is the lapse rate, defined as \(-\frac{(T_L-T_H)}{d}\) (d is the vertical depth of fluid) and \(\kappa\Delta T\) is the thermal diffusion. The last equation of (17) is the mass continuity with Boussinesq approximation. To simplify the problem, we further implement two boundary conditions: (1) \(\mathbf{u}\) = 0 at z=0,d and (2) \(T\) = 0 at z=0,d. In addition, we assume \(\mathbf{u}=(u_x,0,u_z\)). These implemented conditions simplify the Rayleigh-Benard convection to problem of a bounded (at d=0 and z), 2D convection.

We further introduce a few non-dimensional parameters to rescale the equation (,which can be done with Buckingham \(\pi\) theorem as well).

(18)¶\[\begin{split}\begin{align*} x^* &= \frac{x}{d} \\ z^* &= \frac{z}{d} \\ t^* &= \frac{t}{(d^2/\kappa)} \\ u_x^* &= \frac{u_x}{\kappa/d} \\ u_z^* &= \frac{u_z}{\kappa/d} \\ T^* &= \frac{T}{(\kappa\nu/g\alpha d^3)} \\ \end{align*}\end{split}\]

where \(\kappa/d\) is the characteristic velocity and \(t_c\) is the characteristic timescales defined as \((d^2/\kappa)\) (dissipation timescale). With this non-dimensional scaling, (17) is reduced to a set of equations with only two free parameters. In addition, since the solution is 2D and bounded, we can use mass continuity to find the relation between mass stream function and momentum, i.e., \(\mathbf{u}=(u_x,0,u_z)=(-\frac{\partial \psi}{\partial z},0,\frac{\partial \psi}{\partial x})\). This one-on-one relation is so-called invertibility, which is similar to the concept of PV inversion (i.e., (11)).

The x component of (17) contains \(\partial_x p\), and the z component contains \(\partial_z p\). Hence by differentiating the former with respect to z and the latter with respect to x, we have two equations containing a \(\partial_x\partial_z\) term, which drops out on subtraction. Substituting the stream function into this equation results in

(19)¶\[\begin{split}\begin{align*} \partial_{t^*} \Delta^* \psi^*-\partial_{z^*} \psi^* \partial_{x^*} \Delta^* \psi^*+\partial_{x^*} \psi^*\partial_{z^*}\Delta^* \psi^* &= \sigma\Delta^{*2} \psi^*+\sigma\partial_{x^*} T^* \\ \partial_{t^*} T^* -\partial_{z^*} \psi^* \partial_{x^*} T^*+\partial_{x^*} \psi^*\partial_{z^*}T^* &= \Delta^* T^* -R \partial_{x^*} \psi^* \end{align*}\end{split}\]

where \(\sigma\) is Prandlt number, defined as \(\frac{\nu}{\kappa}\), and \(R\) is Rayleigh number, defined as \(\frac{g\alpha d^3 (T_H-T_L)}{\kappa\nu}\). By varying \(\sigma\) and \(R\), we can acquire the statistics of Rayleigh-Bernard convection in different parameter spaces. The animation below is based on a simulation of \((\sigma/R)=\frac{1}{10^8}\) .

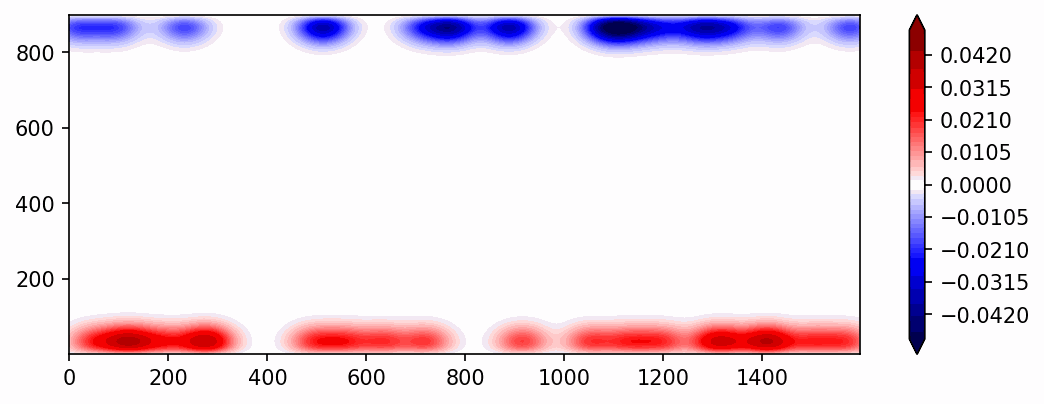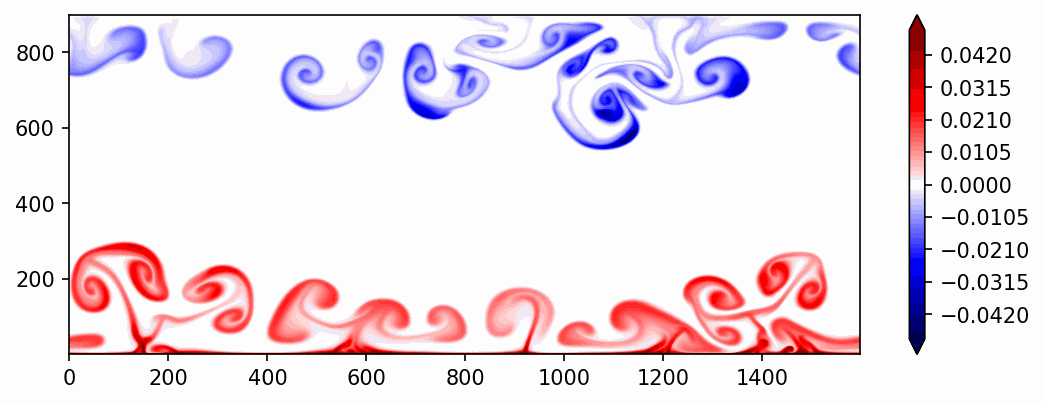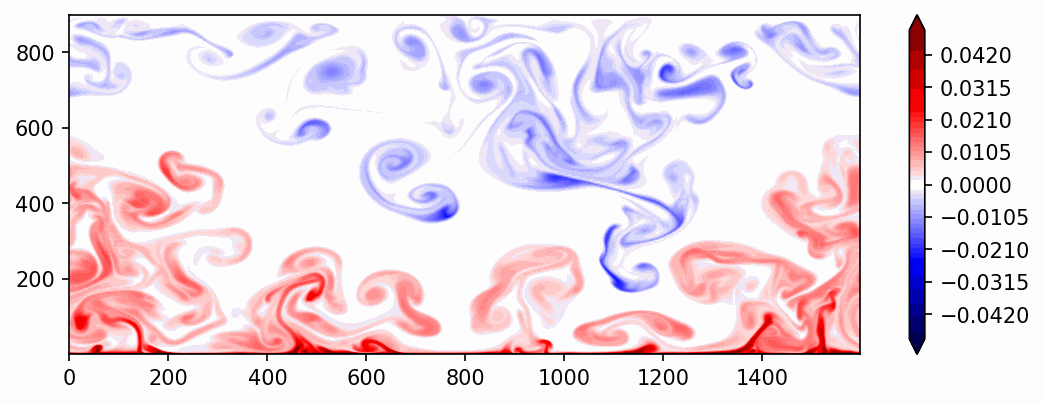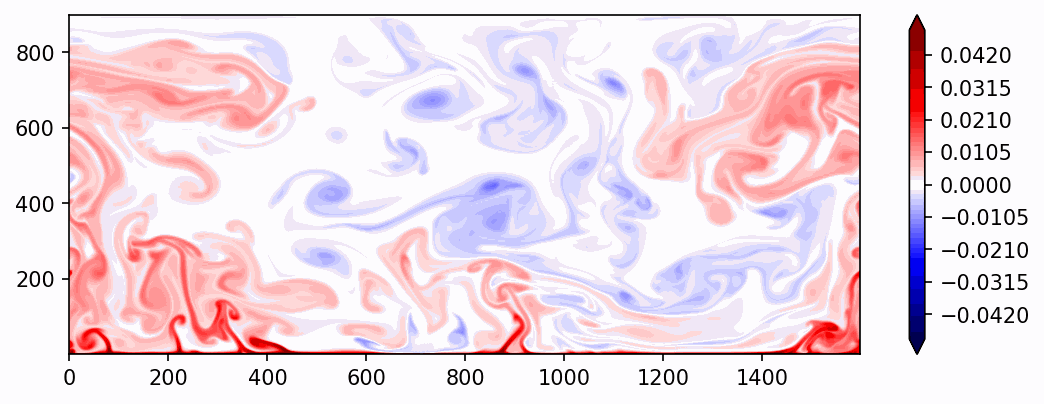
Fig. 6 An example of buoyancy-driven Rayleigh-Barnard convection with \((\sigma/R)=\frac{1}{10^8}\) and an aspect ration of 16:9. (favoring the generation of zonal wave number 2 convection). The shading shows the temperature anomaly.¶

Lorenz 63 model I (solutions)¶

To see if equation (19) can be boiled down to the simplest form but still maintains its chaotic nature, we apply Fourier decomposition to (19) to simplify the problem. Since the solution is periodic in zonal direction but bounded in vertical direction, we assume it has the following form.

(20)¶\[\begin{split}\begin{align*} T^*(x^*,z^*) & = \sum_{k1=-\infty}^{\infty}\sum_{k2=1}^{\infty} \hat{T}_{k1,k2}e^{ik_1\pi x/l} \mathrm{sin}(ik_2\pi z/d)\\ \psi^*(x^*,z^*) & = \sum_{k1=-\infty}^{\infty}\sum_{k2=1}^{\infty} \hat{\psi}_{k1,k2}e^{ik_1\pi x/l} \mathrm{sin}(ik_2\pi z/d) \end{align*}\end{split}\]

Before we dive right in (19), a simple math trick we should know is that the interaction of flow with different scales (i.e., wave number) can yield new scales or new wave number. i.e., \(\psi_{k_1} \psi_{k_2} = \hat{\psi_{k_1}}\hat{\psi_{k_2}}e^{k_1 x}e^{k_2 x}=\hat{\psi_{k_1}}\hat{\psi_{k_1}} e^{(k_1+k_2) x}\). Therefore, to predict \(\psi_{k_1}\) or \(T_{k_1}\) in of (19), we need at least one source term (e.g., advection) which has the same wave number after the nonlinear interaction. Otherwise, we will never be able to predict \(\psi_{k_1}\) or \(T_{k_1}\) due to the orthogonality of Fourier modes (this also leads to another very interesting math problem: Partition, where Srinivasa Ramanujan made some groundbreaking contributions.)

Back to (19), by inspecting (19), the minimum way of sustaining the nonlinearity is to keep the advection term with the least amount of wave numbers. Here we choose the imaginary part of \(\psi_{k_1=1}\) as the starting point. If we drop the advection term in the prognostic equation of \(\psi\) to simplify the equation, the only way to keep its nonlinearity is through \(T\) (since \(\Delta^2 \psi\) is a damping term). Thus, we must have a prognostic equation for \(\hat{T_{k1=1}}\). On the other hand, due to the form of \(\sigma\partial_{x}T\) in (19), the prognostic equation for \(\hat{T_{k1=1}}\) must predict its real part (I will let you think about why).

Because we have dropped the advection term in the prognostic equation of \(\psi\), we must keep the advection term in the prognostic equation of \(T\) to ensure the nonlinearity of the whole dynamical system. According to our previous discussion, as long as the difference in wave number between two scales equals 1 i.e., \(k_1+k_2=1\) or \(k_1-k_2=1\), the nonlinear interaction between \(k_1\) and \(k_2\) can always generate wave number 1 flow. Thus, the simplest way to include the forcing term for \(\hat{T_{k_1=1}}\) without introducing too many new scales is to have \(\hat{T_{k_1=0}}\) since we already have \(\hat{\psi_{k_1=1}}\). (i.e., wave number 1 wind field interacts with the mean temperature). This will bring us the third variable \(\hat{T_{k_1=0}}\).

Let’s take a quick look at what we have so far: the real part of \(\hat{\psi_{k1=1}}\), the imaginary part of \(\hat{T_{k_1=1}}\) and \(\hat{T_{k_1=0}}\). To see if we can close the loop (i.e., enough forcing terms for all included wave numbers), we can substitute \(T\) in (19) with \(\hat{T_{k_1=0}}\) and check if there is any term can be used as the forcing to generate \(\hat{T_{k_1=0}}\). It turned the nonlinear interaction between \(\hat{\psi_{k_1=1}}\) and \(\hat{T_{k_1=1}}\) can yield \(\hat{T_{k_1=0}}\). Thus, we have officially closed the loop!! (Woohoo)

Repeat the same practice, we can find the necessary meridional wave numbers (I will let readers explore this part). Therefore, the solution of (19) is boiled down to

(21)¶\[\begin{split}\begin{align*} \psi^*(x^*,z^*) & = X(t)\mathrm{sin}(\pi ax^*)\mathrm{sin}(\pi z^*) \\ T^*(x^*,z^*) & = Y(t)\mathrm{cos}(\pi ax^*)\mathrm{sin}(\pi z^*)-Z(t)\mathrm{sin}(2\pi z^*) \end{align*}\end{split}\]

where \(a\) is the aspect ratio of domain (i.e., d/l) and \(X(t)\), \(Y(t)\) and \(Z(t)\) correspond to the real part of \(\hat{\psi_{k_1=1,k_2=1}}\), the imaginary part of \(\hat{T_{k_1=1,k_2=1}}\) and \(\hat{T_{k_1=0,k_2=2}}\) respectively. By substituting \(T\) and \(\psi\) in (19) with the definition in (21) and removing the constant. We can have the famous Lorenz 63 model

(22)¶\[\begin{split}\begin{align*} \dot{X} &= -\sigma X+ \sigma Y \\ \dot{Y} &= -XZ+ rX- Y \\ \dot{Z} &= XY- bZ \\ \end{align*}\end{split}\]

where \(\sigma\) is Prandlt number, defined as \(\nu/\kappa\), r is the ratio between \(R\) (Rayleigh number) and \(Rc\) (critical Rayleigh number, defined as \(\pi^4 a^{-2}(1+a^2)^{3}\)) and \(b\) is \(4(1+a^2)^{-1}\) (see more details in [Ray16] and [Sal62]). \(Rc\) provides a mean of estimating if the flow is dominated by buoyancy forcing or turbulent diffusion. When \(R\) is much bigger than \(Rc\), the diffusion is small compared to other terms in (16), thus the small-scale features will take longer to decay (this is the reason why we are more likely to see a turbulent system). In a domain with \(a^2=\frac{1}{2}\), the critical value of \(R\) happens at \(\frac{27\pi^4}{4}\).

From (19) to (22), we can find the Lorenz 63 originated from a heavily truncated Rayleigh-Barnard problem, where the three variables, \(X(t),Y(t)\) and \(Z(t)\) represent the first three Fourier modes.

Lorenz 63 model II (stability analysis)¶

An easy way to visualize how the chosen parameters affect the dynamical behavior in Lorenz 63 model is through the stability analysis. While some basic ideas are provided here, we will cover more details in week 7. The basic concept of linear stability analysis is examining the linear error growth rate and testing if the system is linearly stable or unstable (e.g., \(\psi \sim e^{\lambda t}\), where \(\lambda>0\) for unstable case and vice versa). If the given system is linearly unstable, it will deviate from linear regimes and become unpredictable in finite simulation time.

The linearized Lorenz 63 model can be written as:

(23)¶\[\begin{split}\begin{bmatrix} \dot{X} \\ \dot{Y} \\ \dot{Z} \end{bmatrix} = \begin{bmatrix} -\sigma & \sigma & 0 \\ r & -1 & 0 \\ 0 & 0 & b \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} =\mathbf{L}\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}\end{split}\]

It’s not hard to find that \(Z(t)\) is now decoupled with \(X(t)\) and \(Y(t)\). Interestingly, \(Z(t)\) also represents mean state (wave number 0) in the original Rayleigh-Barnard equation. Physically, linearization also assumes that the mean state doesn’t interact with the transient states.

By calculating the eigen value of \(\mathbf{L}\) in (23), we can estimate the growth rate/frequency of linearized Lorenz 63 model. Since we are looking for a chaotic system, that means we are interested in the case when \(\lambda>0\) (roots are not only real but positive) in (24).

(24)¶\[[\lambda+b][\lambda^2+(\sigma+1)\lambda+\sigma(1-r)]=0\]

(24) has three real roots when \(r>0\); all negative when \(r<1\) and all positive when \(r>1\), which is consistent with the finding in Rayleigh 1912 [Ray16]. (i.e., the convection only happens when \(R>Rc\)). Another way to visualize the linear instability on a phase space is by estimating the divergence of physical states or the trace of the linear operator in (23). i.e., \(\frac{\partial\dot{X}}{\partial X}+\frac{\partial\dot{Y}}{\partial Y}+\frac{\partial\dot{Z}}{\partial Z}=\mathrm{Tr}(\mathbf{L})=-(\sigma+b+1)\) (see discussion in Week 1: Predictability of Weather and Climate). If \(\mathrm{Tr}(\mathbf{L})>0\), it indicates the volume spanned by different ensemble members will increase with the increase of forecast lead time. However, a value of \(\mathrm{Tr}(\mathbf{L})<0\) doesn’t mean this system will shrink to a single point. Instead, it may simply flatten to a plate. In most cases, (24) is not valid due to the non-stationary basic states. A more reasonable way to linearize the Lorenz 63 model will be discussed in week 5 when we talk about its connections with statistical mechanics.

References¶

Lor63: Edward N Lorenz. Deterministic nonperiodic flow. Journal of atmospheric sciences, 20(2):130–141, 1963.
Lor96: Edward N Lorenz. Predictability: a problem partly solved. In Proc. Seminar on predictability, volume 1. 1996.
Ray16(1,2,3): Lord Rayleigh. Lix. on convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 32(192):529–546, 1916.
Sal62(1,2): Barry Saltzman. Finite amplitude free convection as an initial value problem—i. Journal of atmospheric sciences, 19(4):329–341, 1962.

Chaos and Predictability

Week 3: The minimalist models for studying chaos and predictability I: Lorenz 63

Contents