Week 1 and 2: 1st-order ODE¶

What is an ODE¶

For any equation, which shares the form of

(1)¶\[\frac{dy}{dx}=f(x)\]

and x is the only independent variable (or in plain language: coordinate), then it’s called an ordinary differential equation. We can also use different forms to represent the differential terms ex: \(y'\) or \(y^{(n)}\), where n indicates how many times we take the derivative of y with respect to x. An ODE can be found in many places such as calculating the trajectory of a moving object, the temperature/energy change of a system (e.g., how the Earth temperature change in response to greenhouse gas radiative forcing), the transverse circulation of tropical cyclones, the overturning circulation of ITCZ, and even used in a more general concept of dynamical systems. Solving an ODE is exactly finding its integrated form e.g., represent y as a function x without any differential operator (\(\frac{d}{dx}\)).

1st-order ODE¶

According to how many times we take the derivative of y, we can decide the order of differential equations. In general, we are more likely to find the analytical solution in a lower order problem. (and it’s impossible to find an analytical solution when the order is higher than 5. I will leave this question to readers.) Luckily, in most cases, we only need to worry about 1st- and 2nd-order ODEs while higher order problems are relatively rare. More details about how to solve a higher order ODE was covered in Numerical Analysis and the end of this course. Based on the order of ODE, different amounts of boundary (initial) conditions are required. For example, for a moving object with a constant velocity (\(\frac{dx}{dt}=c\)), we need to know where it starts to precisely calculate its path. Otherwise, we can only know how far it travels but have no idea where it ends. From the above example, we can see for an 1st-order ODE, we need at least 1 boundary (initial) condition i.e., \(x_0=?\). Following similar veins, we need 2 initial conditions for a 2nd-order ODE (i.e., \(x^{''}=a\), if \(x^{''}\) represents acceleration, then \(x(t=0)=x_0\) is the initial condition for location and \(x'(t=0)=x'_0\) is the initial velocity) and so on and so forth…

For an 1st-order ODE, we can further categorize it according to its forms, which can help us find the proper way to solve it. Some common forms of 1st-order ODE including (but not limited to):

Forms of ODE

– Separable form: \(\frac{dy}{dx}=F(x)G(y)\)
– Linear form: \(y'+p(x)y=q(x)\)
– Exact form: \(M(x,y)dx+N(x,y)dy=0\) where \(\frac{d M(x,y)}{d y }=\frac{d N(x,y)}{d x }\)
– Homogeneous form: \(y'=f(y/x)\)
– Bernoulli form: \(y'+P(x)y=R(x)y^n\)
– Riccati form: \(y'=P(x)y^2+Q(x)y+R(x)\)

we will walk through each of these in details. One should notice that it is possible to have multiple ways to approach one problem. Categorizing the problems only helps us do it more efficiently but we can certainly solve the problem in different ways.

Categories of 1st-order ODE¶

Separable form¶

For any ODE, which can be rearranged as the following form,

(2)¶\[\frac{dy}{dx}=F(x)G(y)\]

we call it a separable ODE. There is a very straightforward way to solve this kind ODE. We can simply move all of the terms related to y to the left hand side and the terms related to x to the right hand. i.e.,

(3)¶\[\frac{1}{G(y)}dy=F(x)dx\]

by integrating both sides of (3), we can have.

(4)¶\[\int\frac{1}{G(y)}dy=\int F(x)dx\]

The readers can complete the last few steps to derive a form of \(y=f(x)\).

Example 1

Using separable form to solve the following ODE, \(\frac{dy}{dx}=(1-y)x\)

We can first reorganize the equation to have

\[\frac{1}{1-y}dy=xdx\]

then replace \(dy\) with \(d(1-y)\) by using the relation \(d(1-y)=-dy\)

\[-\frac{1}{1-y}d(1-y)=xdx\]

Integrate both side of the equation, we can have

\[\begin{split}-\int\frac{1}{1-y}d(1-y)=\int xdx \\ -\mathrm{ln}(|1-y|) = \frac{1}{2}x^2 + c\end{split}\]

and

\[y = -e^{-\frac{1}{2}x^2+c}+1\]

Example 2

In this example, we will walk through a more practical case: terminal velocity. For a free-falling object, it experiences two forces: gravity (mg) and drag from the air \(\alpha v^2\). Usually, the drag is proportional to the velocity square and counteracts the gravity (hint: we ignore buoyancy here which is a very important term when the falling object has a density close to the air). Therefore, we can write down the following equation to represent balance between different forces

\[m\frac{dv}{dt} = mg-\alpha v^2\]

By rearranging the equation, we can have

\[\frac{1}{1-\frac{\alpha}{gm} v^2}dv = gdt\]

We can partition the left hand side and make it into an integratable form

\[(\frac{\frac{1}{2}}{1+\sqrt{\frac{\alpha}{gm}}v}+\frac{\frac{1}{2}}{1-\sqrt{\frac{\alpha}{gm}}v})dv = gdt\]

and

\[\int (\frac{\frac{1}{2}}{1+\sqrt{\frac{\alpha}{gm}}v}+\frac{\frac{1}{2}}{1-\sqrt{\frac{\alpha}{gm}}v})dv = \int gdt\]

Similarly, using the relation \(d\sqrt{\frac{\alpha}{gm}}v =\sqrt{\frac{\alpha}{gm}}dv\), we can have

\[\frac{1}{2}\sqrt{\frac{gm}{\alpha}} \mathrm{ln}|\frac{1+\sqrt{\frac{\alpha}{gm}}v}{1-\sqrt{\frac{\alpha}{gm}}v}| = gt+c\]

which gives us

\[\frac{1+\sqrt{\frac{\alpha}{gm}}v}{1-\sqrt{\frac{\alpha}{gm}}v} = \mathrm{e}^{2\sqrt{\frac{g\alpha}{m}}t+c'}\]

Rearranging the equation again, we can have the final solution

\[v=\sqrt{\frac{gm}{\alpha}}\frac{\mathrm{e}^{2\sqrt{\frac{g\alpha}{m}}t+c'}-1}{\mathrm{e}^{2\sqrt{\frac{g\alpha}{m}}t+c'}+1}\]

we can test if we derive the right answer by substituting t with \(\infty\). The corresponding velocity is so-called terminal velocity.

Note

when all three forces are all considered (gravity, buoyancy, and drag). It will lead to Rayleigh-Bernard convection, which is an important atmospheric phenomenon. The Lorenz 69 chaos model, also know as the butterfly model, is a reduced dimension of Rayleigh-Bernard convection.

Linear ODE¶

Linear 1st-order ODE is one of the most widely used ODEs in our field, since it’s easy to approach and can be solved (numerically or analytically) in most cases. To tell if an ODE is linear or not, we can simply check its operator.

For example, the following equation

(5)¶\[y'+p(x)y=q(x)\]

we can find that both 3 operators, \(\frac{d}{dx}\), \(p(x)\), and \(q(x)\) are not a function of y. Therefore, this ODE is linear. We can also use traditional way of testing linear operator i.e., \(L(Ay)=AL(y)\), \(L(-y)=-L(y)\), and \(L(y_1+y_2)=L(y_1)+L(y_2)\), where L is the operator that we would like to test, to examine if the whole equation is linear.

For a linear ODE, the easiest way to approach it is using integrating factor. i.e., multiply the whole equation by \(\mathrm{e}^{\int p(x)dx}\). This leads to

(6)¶\[(\mathrm{e}^{\int p(x)dx} y)'=\mathrm{e}^{\int p(x)dx} q(x)\]

By integrating both side of (6) and reorganizing it, we can have the final form

(7)¶\[y =\mathrm{e}^{-\int p(x)dx} \int \mathrm{e}^{\int p(x)dx}+c \mathrm{e}^{-\int p(x)dx}\]

Now let’s take a look of an example in thermodynamics.

Example 3

In the first law of thermodynamics equation, we have

\[c_v \mathrm{dT} = \mathrm{dQ}-\mathrm{Pd\alpha} \]

where \(c_v\) is specific heat in constant volume, \(\mathrm{dQ}\) is the heat exchange, and \(\mathrm{Pd\alpha}\) is the work done by pressure.

Using the relation \(\mathrm{dP\alpha} = \mathrm{Pd\alpha}+\mathrm{\alpha dP}\) as well as the ideal gas law, \(\mathrm{P\alpha}=RT\). we can rewrite the above equation to

\[c_v \mathrm{dT} = \mathrm{dQ}-\mathrm{RdT}+\mathrm{\alpha dP} \]

or

\[c_p \mathrm{dT} = \mathrm{dQ}+\mathrm{RT\frac{dP}{P}} \]

where \(c_p=c_v+R\)

Then divide the whole equation by \(\mathrm{c_p }\), we can have

\[\mathrm{dT} = \frac{1}{\mathrm{c_p}}\mathrm{dQ}+\mathrm{\frac{R T}{c_p}\frac{dP}{P}} \]

By rearranging the equation,

\[\mathrm{dT} - \mathrm{\frac{R}{c_p}\frac{dP}{P}T} = \frac{1}{\mathrm{c_p}}\mathrm{dQ}\]

one can find the integrating factor \(=-\mathrm{\frac{R}{c_p}\frac{dP}{P}}\).

Following the traditions, we multiply the entire equation by \(\mathrm{e}^{\int{-\mathrm{\frac{R}{c_p}\frac{dP}{P}}}}\) or \(\mathrm{e}^{\int{-\mathrm{\frac{R}{c_p}d ln (p)}}}\) and integrate both side to have the final form of thermodynamics equation

\[(T(\frac{P_s}{P})^{\frac{R}{c_p}})'= [\mathrm{e}^{\int{-\mathrm{\frac{R}{c_p}\frac{dP}{P}}}} \frac{1}{\mathrm{c_p}}\mathrm{dQ}]\]

One can easily find that as long as \(dQ=0\) (adiabatic), the left hand side of the equation above is always conserved. This term is called potential temperature, which is a very important thermodynamics variable in atmospheric science.

Exact Form¶

Exact equation is a special type of ODE, where we can’t implicitly write down a solution as a function of independent variable. For example, \(e^{y}sin(x)+2y=x^2\), where no differential form exists. In such case, it is usually impossible to approach the problem using integrating factor or separation of variable

It usually shares the form of

(8)¶\[M(x,y)+N(x,y)y'=0\]

For this type of ODE, we can test if a potential function \(\varphi\) can be found, which satisfies the following definition.

(9)¶\[\begin{split}\begin{align} \frac{\partial \varphi}{\partial x} &= M(x,y) \\ \frac{\partial \varphi}{\partial y} &= N(x,y) \end{align}\end{split}\]

Then solving for the potential function is equivalent to solving the ODE. This can be proofed by substituting \(M(x,y)\) and \(N(x,y)\) in (8) with the definitions in (9), which gives us

(10)¶\[\frac{\partial \varphi}{\partial x}{dx}+\frac{\partial \varphi}{\partial y}{dy} = \frac{d \varphi}{dx}= \varphi^{'}\]

One can carry out the integration of (10) to find the solution.

Here we provide a quick way to test if a potential function exists or not. By inspecting (9), one can easily find that a potential function exists only if \(\frac{\partial M(x,y)}{\partial y}=\frac{\partial N(x,y)}{\partial x}=\frac{\partial ^2 \varphi}{\partial x\partial y}\)

Example 4

Use Exact form to solve the following ODE

\[\frac{dy}{dx}=\frac{2x-\mathrm{e^x sin(y)}}{\mathrm{e^x cos(y)}+1}\]

Let \(M(x,y)=\mathrm{e^x sin(y)}-2x\) and \(N(x,y)=\mathrm{e^x cos(y)}+1\), we can find that \(\frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}\) indicating the existence of a potential function.

To find the corresponding potential function, we can integrate \(M(x,y)\) with respect to \(x\) and \(N(x,y)\) with respect to \(y\) i.e.,

\[\int M(x,y) dx= \mathrm{e^x sin(y)}-x^2+a(y)+c \]

and

\[\int N(x,y) dy= \mathrm{e^x sin(y)}+y+b(x)+c \]

comparing the above two equations, we can see that \(a(y)=y\) and \(b(x)=-x^2\). Therefore, the potential function is \(\mathrm{e^x sin(y)}-x^2+y+c\)

Homogeneous Form¶

In applied math and atmospheric science, you will learn a lot homogeneous terms. All of them have different meanings. In ODE, the homogeneous form indicates that the equation follows a certain form or can be rearranged to a certain form. i.e.,

(11)¶\[y'=f(y/x)\]

When a equation is characterized with the form of (11), we can use separation of equation to solve an ODE. For example, if we let \(u=\frac{y}{x}\), it leads to \(y'=(ux)'=u'x+u=f(u)\). The whole equation can be written as

(12)¶\[u'x+u=f(u)\]

By inspecting (12), we can find that it has a separable form

(13)¶\[\frac{1}{f(u)-u}du=\frac{1}{x}dx\]

and integrate both sides of (13) will yield the final solution.

Example 5

Here we use a pursuit problem as an example. A pursuit problem is widely used in ballistics or calculating the trajectory of a moving object, which is usually subject to a constant forcing e.g., gravity or background flow. It also has some applications in atmospheric sciences when we are calculating the direction of Rossby wave energy dispersion.

Let’s say…if today there is a swimmer who would like to cross a river from point A to point B (see figure below). The current has a constant speed of \(s\). During his swim, he always faced point B (i.e., the angle of \(\alpha\) is changing). \(\mathrm{v}\) is swimmer’s velocity in a vector form. The question is… can we determine the trajectory of the swimmer i.e., y(x).

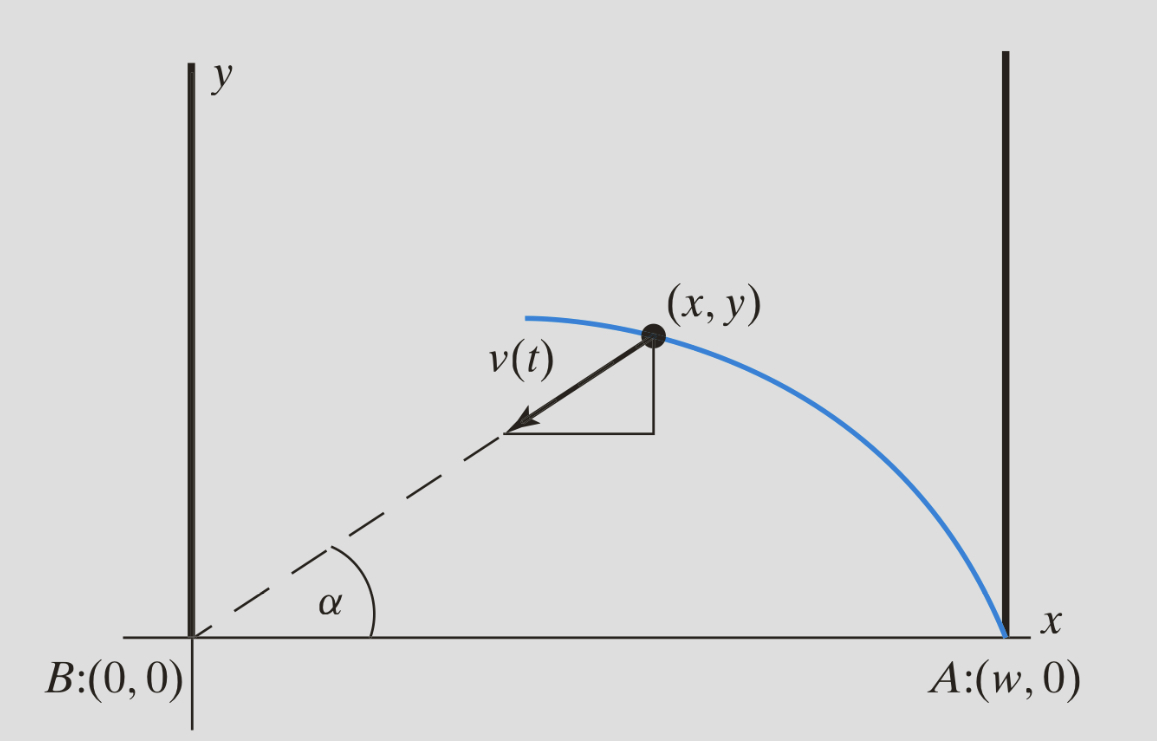
Fig. 1 A schematic figure shows the trajectory of the swimmer.¶

To solve this problem, let’s first write down the information that we already had. First, we know the x velocity and y velocity can be written as:

\[\begin{split}\begin{align} x'(t) &= -v \mathrm{cos}(\alpha) \\ y'(t) &= s-v \mathrm{sin}(\alpha) \\ \end{align}\end{split}\]

by inspecting the equation above, we can find that \(x\) and \(y\) are connected through \(v\) and \(\alpha\). From the FIG1, we also know

\[\begin{split}\begin{align} \mathrm{tan}(\alpha) &= \frac{y}{x} \\ \mathrm{sec}(\alpha) &= \frac{\sqrt{x^2+y^2}}{x} = \sqrt{1+(\frac{y}{x})^2} \end{align}\end{split}\]

Combining all of these equations, we have

\[\frac{dy}{dx} = \frac{y'}{x'} = \frac{s-v \mathrm{sin}(\alpha)}{ -v \mathrm{cos}(\alpha)} = \mathrm{tan}(\alpha)-\frac{s}{v}sec(\alpha) = \frac{y}{x}-\frac{s}{v}\sqrt{1+(\frac{y}{x})^2}\]

Now, we can easily find that it has a homogeneous form, where right hand side is merely a function of \(\frac{y}{x}\).

Let \(y=ux\), and \(y'=u'x+u\), we have

\[u'x+u = u - \frac{s}{v}\sqrt{1+u^2}\]

rearrange the equation

\[\frac{1}{\sqrt{1+u^2}}du = - \frac{s}{v}\frac{1}{x}dx\]

Integrating both side of the equations can give us

\[\mathrm{ln}|\sqrt{1+u^2}+u| = - \frac{s}{v}\mathrm{ln}|x|+c\]

and remove \(\mathrm{ln}\)

\[\sqrt{1+u^2}+u = \mathrm{e}^{- \frac{s}{v}\mathrm{ln}|x|+c} = K\mathrm{e}^{\mathrm{ln}|x|^{-\frac{s}{v}}}=Kx^{-\frac{s}{v}}\]

To obtain \(u\), we can first move \(u\) to the right hand side and take the square of both sides of the equation, which gives us

\[1+u^2 = K^2x^{-2\frac{s}{v}}-2ux^{-2\frac{s}{v}}+u^2\]

and this leads to the final solution

\[u(x) = \frac{1}{2}K x^{-\frac{s}{v}}-\frac{1}{2}\frac{1}{K}x^{\frac{s}{v}}\]

from this, we can obtain

\[y(x) = u(x)x = \frac{1}{2}K x^{1-\frac{s}{v}}-\frac{1}{2}\frac{1}{K}x^{1+\frac{s}{v}}\]

From the boundary value \(y(x=w)=0\), we know \(K=w^{\frac{s}{v}}\)

Bernoulli Form¶

While most of the techniques above can be applied to a linear ODE problem, it is necessary to consider non-linear cases. In general, certain coordinate transformation will be applied to the ODE and make it linear at the first place. The following example is the well-known Bernoulli equation,

(14)¶\[y'+P(x)y=R(x)y^n\]

where n is an integer.

An easy way to make it linear is defining another variable \(v=y^{1-n}\). The derivative of \(v\) is \(v'=(1-n)y^{-n}y'\). This gives us

(15)¶\[\frac{1}{1-n}y^n v'+P(x)y=R(x)y^n\]

or

(16)¶\[v'+(1-n)P(x)v=(1-n)R(x)\]

One can easily find that (15) is a linear ODE which we can approach with integrating factor. By multiplying both sides of equation with \(e^{\int(1-n)P(x)dx}\). We have

(17)¶\[(e^{\int(1-n)P(x)dx}v)'=e^{\int(1-n)P(x)dx}(1-n)R(x)\]

which further leads to

(18)¶\[v=e^{-\int(1-n)P(x)dx} \int e^{\int(1-n)P(x)dx} (1-n)R(x) dx + ce^{-\int(1-n)P(x)dx}\]

Riccati Form¶

Riccati form is another special case of 1st-order ODE, which shares a similar form with Bernoulli differential equation and linear ODE.

(19)¶\[y'=P(x)y^2+Q(x)y+R(x)\]

One can see that when \(P(x)=0\), (19) is linear. On the other hand, if \(R(x)=0\), we will have a Bernoulli equation. Unfortunately, Riccati form can’t be solved with the approaches that we use to solve the other two equations. However, we can take advantage of both approaches. In applied math I, we have learned that if we can find a particular solution, we can get rid of \(R(x)\). As long as we get rid of \(R(x)\), the entire equation can be solved by using the same procedure as we solve the Bernoulli equation.

Based on this concept, we can first assume the solution is the combination of two solutions. Let

(20)¶\[y=S(x)+\frac{1}{z}\]

where \(S(x)\) is a particular solution and \(\frac{1}{z}\) comes from how we solve the Bernoulli form. By substituting (20) into (19), we can have

(21)¶\[S(x)'-\frac{1}{z^2}z' = P(x) (S(x)+\frac{1}{z})^2+Q(x)(S(x)+\frac{1}{z})+R(x)\]

Expand the whole equation and we can see that

(22)¶\[S(x)'-\frac{1}{z^2}z' = P(x) (S(x)^2+2S(x)\frac{1}{z}+\frac{1}{z^2})+Q(x)(S(x)+\frac{1}{z})+R(x)\]

Since \(S(x)\) is a solution of (19), we can rewrite (22) into.

(23)¶\[-\frac{1}{z^2}z' = P(x)(2S(x)\frac{1}{z}+\frac{1}{z^2})+Q(x)\frac{1}{z}\]

By multiplying both sides of equation with \(-\frac{1}{z^2}\) and reorganizing it, we have

(24)¶\[z'+ (2P(x)S(x)+Q(x))z = -P(x)\]

Using integrating factor \(e^{\int 2P(x)S(x)+Q(x) dx}\), we have

(25)¶\[(e^{\int 2P(x)S(x)+Q(x) dx}z)' = -e^{\int 2P(x)S(x)+Q(x) dx} P(x)\]

this will lead to the final solution of z

(26)¶\[z = -e^{-\int 2P(x)S(x)+Q(x) dx} \int e^{\int 2P(x)S(x)+Q(x) dx} P(x) + C e^{-\int 2P(x)S(x)+Q(x) dx}\]

then substitute (26) back to (20), we can have the solution of \(y\)

Applied Math 2

Week 1 and 2: 1st-order ODE

Contents