.md .pdf

repository open issue

Contents

Week 11: Heat Equation

Heat diffusion equation has important applications in engineering and Earth science. Especially when it comes to studying the Earth energy balance. In this chapter, we will consider a very simple 1D thermal diffusion problem. We will also demonstrate that we can always go to higher-dimension problem using separation of variable.

History and Formula

The heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how heat diffuses over a certain material. (later on, the readers will see why the solution of heat diffusion can be approached with Fourier transform.) The heat equation follows a very simple energy conservation law.

(143)\[\textrm{heat change rate} = \textrm{heat flux through boundary to neighbor} + \textrm{forcing}\]

if we write it down in a mathematical form

(144)\[\frac{\partial c(x)\rho(x)u(x,t)}{\partial t} = -\frac{\partial q}{\partial x} + Q(x,t)\]

where \(c(x)\) is the specific heat, \(\rho(x)\) is the density of the stick and \(q\) is the heat flux through the lateral (if other places are insulated) and \(Q(x,t)\) is the local heating source, which can come from molecular process (i.e., friction between atom or radiation). The equation above can be visualized as follow.

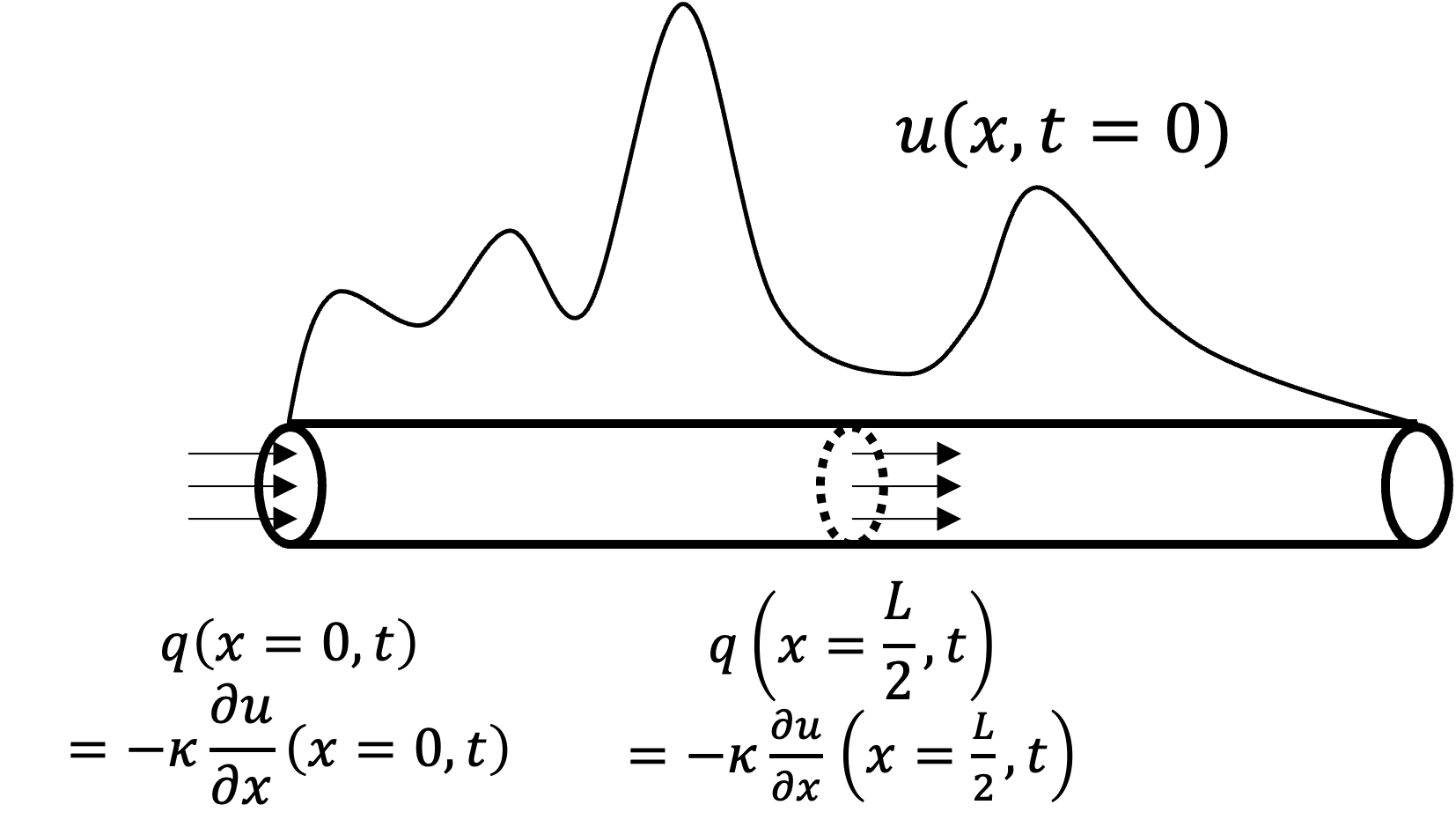
Fig. 15 Heat diffusion on a stick

One can notice that the heat flux is proportional to the temperature difference between the stick and its neighbor, which is the key process in determining the energy redistribution. When there is no temperature gradient (and no external heat source), there is no temperature change. Our goal is to understand how the initial temperature, \(u(x,t)\), evolve as a function of \(x\) and \(t\). In some special cases, we can add convective process (advection) and radiation to the problem but we will keep it simple for now.

(144) can be rewritten as

(145)\[\frac{\partial u}{\partial t} = \kappa_{c} \frac{\partial ^2 u}{\partial x^2}\]

where \(Q(x,t)\) is dropped for simplification and \(\kappa_{c}=\frac{\kappa}{c\rho}\), so-called diffusion coefficient. Again, here we use \(\kappa\) for simplicity.

Considering the solutions are bounded in a stick with \(0\leq x \leq L\). If we closely observe (145), we can find it is the combination of a 1st-order ODE in time and a 2nd-order ODE in space. Therefore, we need at least 1 initial condition and 2 boundary conditions, which usually have form of

(146)\[\begin{split}\begin{align} & u(0,t) = T_1, \; u(L,t) = T_2 \\ & u(x,0) = f(x)\; \textrm{for } \; 0\leq x \leq L \end{align}\end{split}\]

The first two equations of (146) indicates that the temperature at both ends of the stick equals to their nearby environment. We can also use energy constraint where the temperature at both ends are not necessary the same as their environment. Therefore, the temperature difference will cause the heat radiating to its neighbor if the stick has higher temperature than its environment. This can be written as

(147)\[\begin{split}\begin{align} & u_x(0,t) = A[u(0,t)-T], \; u_x(L,t) = -A[u(x,t)-T] \\ & u(x,0) = f(x) \; \textrm{for } \; 0\leq x \leq L \end{align}\end{split}\]

where the \(\pm\) sign simply represents the direction of radiation. One can easily find these two kinds of boundary condition fall within the category of type I Sturm-Liouville problem. It’s also possible to have a mixed boundary condition, where

(148)\[\begin{split}\begin{align} & u_x(0,t) = T_1, \; u_x(L,t) = -A[u(x,t)-T_2] \\ & u(x,0) = f(x) \; \textrm{for } \; 0\leq x \leq L \end{align}\end{split}\]

or vice versa.

Now let’s take a look of a few cases.

Example 1

First consider the problem

\[\begin{split}\begin{align} & u_t = \kappa_{c} u_{xx} \; \textrm{for } \; 0\leq x \leq L \\ & u(0,t) = u(L,t) = 0 \\ & u(x,0) = f(x) \end{align}\end{split}\]

Using separation of variable of as what we did in previous chapter, consists of attempting a solution of the form

\[\begin{align} u(x,t) = X(x)T(t) \end{align}\]

Substitute this into the differential equation to get

\[\begin{align} XT^{'} = \kappa_{c}X^{''}T \end{align}\]

which is equivalent to

\[\begin{align} \frac{T^{'}}{\kappa_{c}T} = \frac{X^{''}}{X} \end{align}\]

Observing the equation above, we can find the left hand side only depends on \(t\) and the right hand side only depends on \(x\). We also know that \(X(x)\) and \(T(t)\) vary independently. Therefore, only possibility exists: the ration of \(T^{'}\) and \(kT\) is a constant and so do \(X^{''}\) and \(X\). According to this, we can write down

\[\begin{align} \frac{T^{'}}{\kappa_{c}T} = \frac{X^{''}}{X} = -\lambda \end{align}\]

One should notice that we can choose \(lambda\) on the right in stead. However, to satisfy the Fourier solution is space, we can only have \(-\lambda \). (readers can think about why?).

Now we have two differential equations. For the spatial structure equation,

\[\begin{align} & X^{''} + \lambda X = 0 \; \textrm{with } X(0) = X(L) = 0 \end{align}\]

The first equation has a solution of Fourier \(\sin\) function,

\[\begin{split}\begin{align} & X_n(x) = \sin(\frac{n\pi x}{L}) \; \textrm{for } n=1,2,\cdots \\ & \textrm{where} \lambda =\frac{n^2\pi^2}{L^2} \end{align}\end{split}\]

For the temporal structure equation,

\[\begin{align} & T^{'} + \kappa_{c}\frac{n^2\pi^2}{L^2} T = 0 \end{align}\]

This implies

\[\begin{align} T = e^{-\kappa_{c}\frac{n^2\pi^2}{L^2}t} \end{align}\]

Put two solutions together, we have

\[\begin{align} u(x,t) = \sum_{n=1}^{\infty} b_n \sin(\frac{n\pi x}{L})e^{-\kappa_{c}\frac{n^2\pi^2}{L^2}t} \end{align}\]

where

\[\begin{align} u(x,0) = \sum_{n=1}^{\infty} b_n \sin(\frac{n\pi x}{L}) = f(x) \end{align}\]

\(b_n\) is the Fourier \(\sin\) coefficients for each Fourier mode, which can be derived by projecting \(f(x)\) onto different Fourier basis

\[b_n = \frac{2}{L}\int_{0}^{L}f(x)\sin(\frac{n\pi x}{L}) dx\]

and the final solution is

\[\begin{align} u(x,t) = \sum_{n=1}^{\infty} (\frac{2}{L}\int_{0}^{L}f(\xi)\sin(\frac{n\pi \xi}{L}) d\xi) \sin(\frac{n\pi x}{L})e^{-\kappa_{c}\frac{n^2\pi^2}{L^2}t} \end{align}\]

From the solution above, one can find it will gradually approach 0 when \(t\rightarrow\infty\) because of \(e^{-\kappa_{c}\frac{n^2\pi^2}{L^2}t}\). This is consistent with physical intuition. Therefore, for a heat diffusion without the existence of external forcing, the solution will gradually be smoothed out.

Example 2: Diffusion on an Insulated Stick

Now considering a case where we have temperature gradient on a insulated stick. The first half has temperature of \(T\) and the second half has temperature \(0\).

\[\begin{split}f(x) = \begin{cases} T \textrm{ for } 0\leq x \leq \frac{L}{2}\\ 0 \textrm{ for } \frac{L}{2}< x \leq L\\ \end{cases}\end{split}\]

Given the entire stick is insulated, we can expect that the equilibrium temperature will be \(\frac{T}{2}\) i.e., half of the heat moves from the left to the right. In addition, the insulated stick will have Fourier \(\cos\) function as solution given 0 radiation boundary condition. i.e.,

\[u_x(0,t) = u_x(L,t) = 0\]

The equation above can be considered as that the environment and stick always have the same temperature which leads to 0 heat exchange between sticks and outside environment. For such condition, the solution has a form of Fourier \(\cos\) function. Therefore, the solution can be written as

\[\begin{align} u(x,t) = \sum_{n=0}^{\infty} a_n \cos(\frac{n\pi x}{L})e^{-\kappa_c\frac{n^2\pi^2}{L^2}t} \end{align}\]

To get the Fourier coefficient,

\[a_n = \frac{2}{L} \int^{\frac{L}{2}}_{0} T \cos(\frac{n\pi x}{L}) dx = \frac{2T}{n\pi}\sin(\frac{n\pi}{2})\]

where

\[a_0 = \frac{T}{2}\]

The solution can be written as

\[\begin{align} u(x,t) = \frac{T}{2}+\frac{2T}{\pi}\sum_{n=1}^{\infty} \frac{1}{n}\sin(\frac{n\pi}{2}) \cos(\frac{n\pi x}{L})e^{-\kappa_{c}\frac{n^2\pi^2}{L^2}t} \end{align}\]

One can see that \(k\) only appears in \(e^{-\kappa_{c}\frac{n^2\pi^2}{L^2}t}\). If we choose a \(k\) big enough, the signal will flatten out very quickly.

From two cases above, the readers can extend to some more complicated cases such as one side has a constant temperature and the other side is radiation boundary condition. I will leave the practice to the readers.

Example 3: Nonhomogeneous Problem

Solve the following case,

\[\begin{split}\begin{align} & u_t = ku_{xx} \; \textrm{for } \; 0\leq x \leq L \\ & u(0,t) = T_1 \\ & u(L,t) = T_2 \\ & u(x,0) = f(x) \end{align}\end{split}\]

where either \(T_1\) or \(T_2\) is not 0 (and \(T_1\neq T_2\)). Such case can be considered as a nonhomogeneous case. Because the temperature on both ends are different, there is always heat moving from one side to the other side. Thus, this problem is equivalent to a problem with a constant forcing. The simplest way of doing that is assuming \(u(x,t)\) has the following form

\[\begin{align} u(x,t) = v(x,t) + \psi(x) \end{align}\]

where \(\psi(x)\) can take care of the nonhomogeneous temperature of the stick and \(v(x,t)\) will to lead a homogeneous problem. i.e.,

\[\begin{split}\begin{align} & v_t = kv_{xx}+ \psi_{xx}(x); \textrm{for } \; 0\leq x \leq L \\ & v(0,t) = 0 \\ & v(L,t) = 0 \\ & v(x,0) = f(x) \end{align}\end{split}\]

to make the set of equation above homogeneous, we have \(\psi_{xx}(x)=0\). This implies \(\psi(x) = Ax+B\). Using the boundary condition, \(\psi(0) = B = T_1\) and \(\psi(L) = AL+T_1 = T_2\), we know \(\psi(0) = (T_2-T_1)x/L+T_1\). To solve \(v\), we can follow the same steps in example 1.

Example 4: Inclusion of Convection and other Processes

We can include convection and other processes,

\[\begin{split}\begin{align} & u_t = (ku_{xx}+Au_x+Bu) \; \textrm{for } \; 0\leq x \leq L \\ & u(0,t) = u(L,t) = 0 \\ & u(x,0) = f(x) \end{align}\end{split}\]

We can first convert it to a form which we are familiar with

\[\begin{split}\begin{align} & v_t = kv_{xx} \; \textrm{for } \; 0\leq x \leq L \\ & v(0,t) = v(L,t) = 0 \\ & v(x,0) = g(x) \end{align}\end{split}\]

Recall that solving the 1st/2nd-order ODE, we usually guess a solution of \(e^{\alpha x+\beta t}\) to get a characteristic equation. However, it doesn’t satisfy the boundary condition where \(u(0,t) = u(L,t) = 0\). Therefore, we can use the same approach of variation of parameters and assume

\[\begin{align} u(x,t) = v(x,t)e^{\alpha x+\beta t} \end{align}\]

which will lead to

\[\begin{split}\begin{align} & u_t(x,t) = \beta v(x,t)e^{\alpha x+\beta t}+v_t(x,t)e^{\alpha x+\beta t} \\ & u_x(x,t) = \alpha v(x,t)e^{\alpha x+\beta t}+v_x(x,t)e^{\alpha x+\beta t} \\ & u_xx(x,t) = \alpha^2 v(x,t)e^{\alpha x+\beta t}+2\alpha v_x(x,t)e^{\alpha x+\beta t} + v_xx(x,t)e^{\alpha x+\beta t} \\ \end{align}\end{split}\]

and

\[\begin{align} & \beta v(x,t) = (k\alpha^2+kA\alpha-\beta+kB)v+(2k\alpha+kA)v_x+kv_{xx} \end{align}\]

The equation above implies

\[\begin{split}\begin{align} & k\alpha^2+kA\alpha-\beta+kB = 0 \\ & 2k\alpha+kA = 0 \end{align}\end{split}\]

or

\[\begin{split}\begin{align} & \alpha = -\frac{A}{2} \\ & \beta = k(B-\frac{A^2}{4}) \end{align}\end{split}\]

With the chosen \(\alpha\) and \(\beta\), we can reorganize the original equation to a solvable form.

Forced Solutions

While (145) takes heat flux as the only process for redistributing heat, we can have additional heat sources, \(F(x,t)\). Therefore, (145) is written as

(149)\[\begin{split}\begin{align} & \frac{\partial u}{\partial t} = k \frac{\partial ^2 u}{\partial x^2}+F(x,t) \; \textrm{for } \; 0\leq x \leq L \\ & u(0,t) = u(L,t) = 0 \\ & u(x,0) = f(x) \end{align}\end{split}\]

It is easy to verify that separation of variables can be applied to the questions above when \(F(x,t)\) exist. However, we can do some scale analysis first… One can find that when \(F(x,t)\) is small, we can expect the solution has a form of Fourier \(\sin\) function. i.e.,

(150)\[\begin{align} u(x,t) = \sum_{n=0}^{\infty} b_n \sin(\frac{n\pi x}{L})e^{-n^2\pi^2 kt/L^2} \end{align}\]

with the numbers the Fourier \(\sin\) coefficients of \(f(x)\). This suggests that, for the problem with the term of \(F(x,t)\), attempt a solution

(151)\[\begin{align} u(x,t) = \sum_{n=0}^{\infty} T_n(t) \sin(\frac{n\pi x}{L}) \end{align}\]

because the spatial structure is constrained by both ends, which ensures the solution is the linear combination of Fourier \(\sin\) functions. According to (151), one can find that \(T_n(t)\) is simply the coefficients of Fourier \(\sin\) functions. i.e.,

(152)\[\begin{align} T_n(t) = \frac{2}{L}\int_{0}^{L} u(\xi,t) \sin(\frac{n\pi \xi}{L})d\xi \end{align}\]

Following similar veins, we take Fourier transform of the entire heat diffusion equation, which leads to

(153)\[\begin{split}\begin{align} T_n^{'}(t) & = \frac{2k}{L}\int_{0}^{L} u_{xx}(\xi,t) \sin(\frac{n\pi \xi}{L})d\xi + \frac{2}{L}\int_{0}^{L} F(\xi,t) \sin(\frac{n\pi \xi}{L})d\xi \\ & = \frac{2k}{L}\int_{0}^{L} u_{xx}(\xi,t) \sin(\frac{n\pi \xi}{L})d\xi + B_n(t) \end{align}\end{split}\]

where

(154)\[\begin{align} B_n(t) = \frac{2}{L}\int_{0}^{L} F(\xi,t) \sin(\frac{n\pi \xi}{L})d\xi \end{align}\]

Evaluate the last integral in (153) by carrying out two integrate by parts.

(155)\[\begin{split}\begin{align} \frac{2k}{L}\int_{0}^{L} u_{xx}(\xi,t) \sin(\frac{n\pi \xi}{L})d\xi &= \frac{2k}{L}([u_{x}(\xi,t)\sin(\frac{n\pi \xi}{L})]_{0}^{L}-\frac{n\pi}{L}\int_{0}^{L}u_{x}\cos(\frac{n\pi \xi}{L})d\xi) \\ &=0-\frac{2k n\pi}{L^2}[[u\cos(\frac{n\pi \xi}{L})]_{0}^{L}+\frac{n\pi}{L}\int_{0}^{L}u\sin(\frac{n\pi \xi}{L})d\xi] \\ &=-\frac{2k n\pi}{L^2} \frac{n\pi}{L}\frac{L}{2}T_n \\ &=-\frac{k n^2\pi^2}{L^2}T_n \end{align}\end{split}\]

substitute this result back to (153), we have

(156)\[\begin{align} T_n^{'}(t) + \frac{k n^2\pi^2}{L^2}T_n(t) = B_n(t) \end{align}\]

which is a solvable 1st-order ODE.

With an initial condition of

(157)\[\begin{align} T_n(0) = b_n \end{align}\]

we can find the solution for \(T_n\)

(158)\[\begin{align} T_n(t) = \int_{0}^{t} e^{-\frac{kn^2\pi^2(t-\tau)}{L^2}}B_n(\tau)d\tau+b_ne^{-\frac{kn^2\pi^2(t)}{L^2}} \end{align}\]

and the final solution is

(159)\[\begin{align} u(x,t) = \sum_{n=0}^{\infty} \int_{0}^{t} e^{-\frac{kn^2\pi^2(t-\tau)}{L^2}}B_n(\tau)d\tau \sin(\frac{kn\pi}{L}x)+\sum_{n=0}^{\infty}b_ne^{-\frac{kn^2\pi^2(t)}{L^2}}\sin(\frac{kn\pi}{L}x) \end{align}\]

Solutions on a Real String

For certain cases, the heat diffusion does not necessarily happen on a stick or a string but instead…over an infinite domain. We first start with finite domain Fourier transform, where the solution are bounded in \([-L,L]\). Sturm-Liouville theorem tells us that the solution has a form of:

(160)\[\begin{split}\begin{align} f(x) &= \sum_{n=0}^{\infty} a_n\cos(\frac{n\pi x}{L})+b_n\sin(\frac{n\pi x}{L}) \\ &= \sum_{n=0}^{\infty} a_n\cos(k_n x)+b_n\sin(k_n x) \; n\in \mathbb{Z} \textrm{ and }\; \; k\in \mathbb{R} \end{align}\end{split}\]

It is equivalent to

(161)\[\begin{align} f(x) = \sum_{n=-\infty}^{\infty} c_n e^{\frac{i n\pi x}{L}} = \sum_{n=-\infty}^{\infty} c_n e^{i k(n) x} \; n\in \mathbb{N} \textrm{ and }\; \; k\in \mathbb{R} \end{align}\]

where

(162)\[\begin{split}\begin{align} c_n & = \frac{a_n-ib_n}{2} =\frac{\int_{-L}^{L} f(x)e^{-ikx} dx}{\int_{-L}^{L} |e^{-ikx}|^2 dx} = \frac{1}{2L} \int_{-L}^{L} f(x)e^{-ikx} dx \\ a_n & = \frac{1}{L} \int_{-L}^{L}f(x)\cos(\frac{n\pi x}{L}) dx = \frac{1}{L} A_n\\ b_n & = \frac{1}{L} \int_{-L}^{L}f(x)\sin(\frac{n\pi x}{L}) dx = \frac{1}{L} B_n\\ \end{align}\end{split}\]

Here we introduce a small trick. If we let \(L\rightarrow\infty\), we will have \(\delta k = k(n+1)-k(n-1) = \frac{\pi}{L} \sim 0 \). One should notice that, infinite size of domain is equivalent to a limited size domain with infinite wave numbers. Therefore,

(163)\[\begin{split}\begin{align} f(x) &= \frac{1}{2L}\sum_{n=-\infty}^{\infty} (A_n-iB_n) e^{ikx} \\ &= \frac{1}{2\pi}\sum_{n=-\infty}^{\infty} (A_n-iB_n) e^{ikx} \Delta k\\ &= \int_{k=-\infty}^{\infty} \frac{1}{2\pi}F(k) e^{i k x} dk\; k\in \mathbb{R} \end{align}\end{split}\]

and

(164)\[\begin{align} F(k) = \int_{-L \rightarrow -\infty}^{L \rightarrow \infty} f(x)e^{-ikx} dx =\mathcal{F}[f(x)] \end{align}\]

(164) is the Fourier transform of \(f(x)\) over an infinite domain.

Now we can use the Fourier transform in an infinite domain to solve the heat diffusion equation.

Example 4

Solve

\[\begin{split}\begin{align} u_t & = \kappa_c u_{xx} \;\;\textrm{for }\infty<x\infty, t>0 \\ u(x,0) & =f(x) \end{align}\end{split}\]

Now we take Fourier transform with respect to space.

\[\begin{split}\begin{align} \mathcal{F}[u(x,t)] & = \hat{u}(k,t) \\ \mathcal{F}[u_x(x,t)] & = ik \hat{u}(k,t) \\ \mathcal{F}[u_{xx}(x,t)] & = -k^2 \hat{u}(k,t) \\ \end{align}\end{split}\]

where \(\hat{u}\) is \(u\) in wave number space.

This leads to

\[\begin{align} \frac{d}{dt} \hat{u} = -\kappa_c k^2 \hat{u}(k,t) \end{align}\]

and the solution is

\[\begin{align} \hat{u}(k,t) = \hat{u}(k,0)e^{-\kappa_c k^2 t} \end{align}\]

\(e^{-\kappa_c k^2 t} \) is so-called diffusion kernel, which is a Gaussian function.

Then we take the inverse transform of the equation above,

\[\begin{align} \mathcal{F}^{-1}[\hat{u}(k,t)] = \mathcal{F}^{-1}[\hat{u}(k,0)e^{-\kappa_c k^2 t}] = \mathcal{F}^{-1}[\hat{u}(k,0)]*\mathcal{F}^{-1}[e^{-\kappa_c k^2 t}] \end{align}\]

One interesting fact is, the inverse Fourier transform of a Gaussian function is also a Gaussian function. (I will leave this practice to readers).

\[\begin{align} \mathcal{F}^{-1}[e^{-\kappa_c k^2 t}] = \frac{1}{2\sqrt{\kappa_c \pi t}}e^{-\frac{x^2}{4\kappa_c t}} \end{align}\]

The entire solution is

\[\begin{align} u(x,t) = \frac{1}{2\sqrt{\kappa_c \pi t}}e^{-\frac{x^2}{4\kappa_c t}}*u(x,0) \end{align}\]

Heat Diffusion on a 2D Plane

Thus far we have considered the heat equation in one space variable. In two space dimensions the heat equation is

(165)\[\begin{align} u_t = \kappa_c (u_{xx}+u_{yy}) \end{align}\]

Suppose that we want a temperature distribution on a square plate occupying the regions of \(0\leq x\leq L\) and \(0\leq y\leq K\). A zero environmental temperature condition is given i.e.,

(166)\[\begin{split}\begin{align} u(x,0,t) & = u(x,K,t) = 0 \\ u(0,y,t) & = u(L,y,t) = 0 \\ \end{align}\end{split}\]

also assume an initial condition,

(167)\[\begin{align} u(x,y,0) = f(x,y) \end{align}\]

We first attempt separation of variables in the heat equation, putting \(u(x,y,t) = X(x)Y(y)T(t)\) to get

(168)\[\begin{align} XYT' = \kappa_c(X^{''}YT+XY^{''}T) \end{align}\]

Divide by \(XYT\) and rearrange the equation

(169)\[\begin{align} \frac{X^{''}}{X} = \frac{T^{'}}{\kappa_c T}-\frac{Y^{''}}{Y} \end{align}\]

while the left-hand-side of the equation only depends on \(X\) and right-hand-side of the equation only depends on \(T\) and \(Y\). That means both side of the equation will equal to the same constant. This is the only way that two independent equations are always equivalent.

indicating

(170)\[\begin{align} \frac{X^{''}}{X} = \frac{T^{'}}{\kappa_c T}-\frac{Y^{''}}{Y}=-\lambda \end{align}\]

or

(171)\[\begin{split}\begin{align} X^{''}+\lambda X & = 0 \\ \frac{T^{'}}{\kappa_c T}+\lambda &= \frac{Y^{''}}{Y} \end{align}\end{split}\]

Similarily, the second equation also implies

(172)\[\begin{align} \frac{T^{'}}{\kappa_c T}+\lambda &= \frac{Y^{''}}{Y} = \mu \end{align}\]

Now,

(173)\[\begin{split}\begin{align} Y^{''}+\mu Y & = 0 \\ T^{'}+(\lambda+\mu)\kappa_cT & = 0 \\ \end{align}\end{split}\]

Along with the boundary conditions, we know the eigen solutions for X and Y ares

(174)\[\begin{split}\begin{align} X_n(x) = \sin(\frac{n\pi x}{L}) ;\ \textrm{where } n=1,2,3... \\ Y_n(x) = \sin(\frac{m\pi x}{K}) ;\ \textrm{where } m=1,2,3... \\ \end{align}\end{split}\]

Also, the solutions for T are

(175)\[\begin{align} T_{nm} (t) = e^{-\alpha_{nm}t} ;\ \textrm{where } \alpha = \frac{n^2\pi^2}{L^2}+\frac{m^2\pi^2}{K^2} \end{align}\]

Combining all three solutions together, we can have the final solution of heat diffusion on a 2D-plane. The readers can also try to think about the forced solution on a 2D-plane. What should it look like?

previous

Week 9 and 10: Special Functions

next

Week 12: Wave Equation