Week 7 and 8: Sturm-Liouville Theorem: Eigenfunctions and Fourier Series¶

Sturm-Liouville form¶

Sturm-Liouville Theorem is named after two great mathematicians, Jacques Charles François Sturm (1803-1855) and Joseph Liouville (1809–1882). Jacque Charles François Sturm first described how an ordinary differential equation satisfies a certain form can be solved by separation of variables and he used a thermal diffusion in a thin bar as an example. However, during that period, people were more interested in the general solution of that given math problem. The most important contribution from Jacques Charles François Sturm and Joseph Liouville was applying the eigen function approach to find the general solution of ODEs with a certain form. Later on, people called it Sturm-Liouville Theorem. In addition to the contribution in differential equation, Joseph Liouville was also famous for his achievement in statistical mechanisms and dynamical systems. We will cover more details in another course Chaos and Predictability.

The solution of Sturm-Liouville form plays an important role in modeling wave and thermal diffusion. Since the Sturm-Liouville era, mathematicians and engineers have found a lot of scientific problems sharing the Sturm-Liouville form, such as Bessel Function, Parabolic Cylinder functions, Hermite Polynomial, Legendre Polynomial, and even the Fourier Series, where we can find a set of eigen functions spanning the entire solution space. These have been applied to find the solution of tropical wave, transverse circulations of ITCZ and hurricane, and the equilibrium temperature of Earth.

Mathematically, the Sturm-Liouville form can be written as

(80)¶\[y^{''}+R(x)y^{'}+(Q(x)+\lambda P(x))y = 0\]

using integrating factor, we can multiply the entire equation by

(81)¶\[r(x) = e^{\int R(x) dx}\]

to obtain

(82)¶\[e^{\int R(x) dx}y^{''}+R(x)e^{\int R(x) dx}y^{'}+(Q(x)e^{\int R(x) dx}+\lambda P(x)e^{\int R(x) dx})y = 0\]

or

(83)¶\[(r(x)y^{'})^{'}+(q(x)+\lambda p(x))y = 0 \]

where $r(x)=e^{\int R(x) dx}$, $q(x)=Q(x)e^{\int R(x) dx}$, and $p(x)= P(x)e^{\int R(x) dx}$. Here, we can setup some extreme cases and test what we can find.

Let $r(x)=1$, $q(x)=0$, and $p(x)$ is a constant. In addition, we have two simple boundary conditions: $y(0)=0$ and $y(1)=0$. The entire equation is reduced to

(84)¶\[y^{''}+\Lambda y \Longrightarrow Ly=-\Lambda y\]

where $L=\frac{d^2}{dx^2}$. (84) has a set of solution

(85)¶\[y=c_1e^{ax}\cos(bx)+c_2e^{ax}\sin(bx)\]

where $b=\sqrt{\Lambda}$ (one should notice that we assume $\Lambda>0$, more details are provided in the discussion about Fourier Series). If we substitute boundary conditions into (85), one can find $a=0$, $c_1=0$, and $c_2\sin(\sqrt{\Lambda})=0$. Since we don’t want a trivial solution (i.e., both $c_1$ and $c_2$ are 0), it implies that $\sin(\sqrt{\Lambda})=0$. For $\sin$ function, we can find 0 solution at each multiple $\pi$ suggesting $\sqrt{\Lambda}=n\pi$, where $n$ is an integer. This gives as the final form of solution

(86)¶\[y=c_2\sin(n\pi x); \; n\in \mathbb{Z} \]

(86) is the famous Fourier $\sin$ function. If one looks closely to (84), it is actually an eigen value problem as long as $L$ is a Hermitian operator (or matrix). Indeed, we can prove the differential operator is an Hermitian operator. It also implies that the eigen functions span the entire solution space and any solution can be the linear combination of the eigen functions. At this moment, readers probably can figure out two most important things in this chapter: (1) what functions share Sturm-Liouville form, and (2) how to find the eigen basis.

Note

The Hermitian matrix or operator is defined as a self-adjoint matrix (operator) where the eigen functions span the entire vector space of solution. Mathematically, it has a few unique characteristics. First, we can swap the order the operator without changing the results

\[\langle Ax,y \rangle = \langle x,Ay \rangle; \; \textrm{where $\langle,\rangle$ is the inner product} \]

Second, all of the eigen values from a self-adjoint matrix (operator) are real. Third, all of the eigen vectors from a self-adjoint matrix (operator) are orthogonal.

For the first question, any equation satisfies the form (80) (where $R(x)$, $P(x)$, and $Q(x)$ are continuous over the domain of interest) and one of the any following boundary conditions, is a Sturm-Liouville form.

Boundary Conditions

Type I: Regular Sturm-Liouville Problem

\[a_1y(a)+a_2y^{'}(a)=0;\; \textrm{and}\; b_1y(b)+b_2y^{'}(b)=0; \;\; \textrm{with $a_1$ ($b_1$) and $a_2$ ($b_2$) are not both 0} \]

Type II: Periodic Sturm-Liouville Problem

\[y(a)=y(b);\;\textrm{and};\; y^{'}(a)=y^{'}(b)\]

Type III: Singular Sturm-Liouville Problem

\[r(a)=0;\; \textrm{or}\; r(b)=0\]

when $r(a)=0$, we need $b_1y(b)+b_2y^{'}(b)=0$ with $b_1$ and $b_2$ not both 0. Similar boundary conditions applied to point $a$.
when $r(b)=0$, we need $a_1y(a)+a_2y^{'}(a)=0$ with $a_1$ and $a_2$ not both 0.

There are a few important characteristics for Sturm-Liouville problem.

For types I and II, the Sturm-Liouville problem has an infinite number of distinct eigen values $\Lambda_n$ (some textbooks use $\lambda_n$). If these are labeled with increasing order. i.e., $\lim_{n\rightarrow\infty} \Lambda_n=\infty$
The eigen value of Sturm-Liouville is real since it’s operator is Hermitian.
For any Sturm-Liouville problem, any non-zero multiple of an eigenfunction is also an eigenfunction corresponding to the same eigen value.
For a regular Sturm-Liouville, any two eigen function correspond to the same eigen value must be the be a nonzero multiple of each others. While it’s not the case for periodic Sturm-Liouville.

For the second question: how to find proper eigenfunctions, we will walk through a special case with $r(x)=1$, $q(x)=0$, and $p(x)$ with type I or II boundary conditions and leave more general cases in the chapter of special functions.

Example 1

Find the solution of the following ODE

\[y^{''}+\lambda y =0; \; y(-L)=y(L); \;y^{'}(-L)=y^{'}(L)\]

from (85) with $\lambda>0$ (I will let readers try two other cases), we know the general solutions are written

\[y=c_1\cos(\sqrt{\lambda}x)+c_2\sin(\sqrt{\lambda}x)\]

and the second order derivative

\[y^{''}=-c_1\lambda\cos(\sqrt{\lambda}x)-c_2\lambda\sin(\sqrt{\lambda}x)\]

Substituting the boundary into the equations above,

\[y(L)=c_1\cos(\sqrt{\lambda}L)+c_2\sin(\sqrt{\lambda}L)=y(-L)=c_1\cos(\sqrt{\lambda}L)-c_2\sin(\sqrt{\lambda}L)\]

This implies that $c_2\sin(\sqrt{\lambda}L)=0$, and $\sqrt{\lambda}L=n\pi$. Also, the boundary conditions from the derivative term give us the same conclusion. Therefore, the general solution is

\[y(L)=c_1\cos(\frac{n\pi}{L}x)+c_2\sin(\frac{n\pi}{L}x)\]

Example 2

Find the solution of

\[y^{''}+\lambda y =0; \; y(0)=0; \;y^{'}(L)+Ay(L)=0\]

where $A$ is a positive constant. This problem occurs in solving for the temperature of a homogeneous bar, which radiates energy from on end to the surrounding medium.

Following the example above, we know the equation has a general solution of

\[y(x)=c_1\cos(kx)+c_2\sin(kx)\]

Substituting the boundary conditions into the equation gives us $c_1=0$.

\[\begin{split}\begin{align} y^{'}(L)+Ay(L) &= c_2 k \cos(kL) + Ac_2\sin(kL) \\ &= c_2(k \cos(kL)+A\sin(kL)) \\ &= 0 \end{align}\end{split}\]

since we don’t want trivial solution (i.e., $c_2=0$), indicating

\[\tan(kL)=-\frac{k}{A}\]

Let $kL=z$, we have

\[\tan(z)=-\frac{z}{AL}\]

and $z$ is the eigen value.

To visualize the solution,

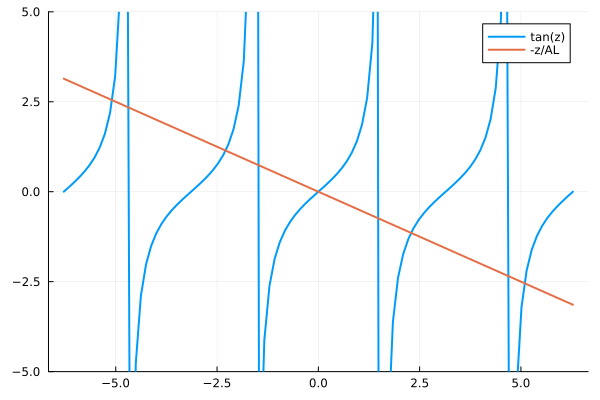
Fig. 7 The solutions of ODE. x-axis represents z in the solution above. The z coordinate of the cross-section between $\tan(z)$ and $-\frac{z}{AL}$ is the eigen value of given solutions.¶

Eigenfunction Expansions¶

Recall that for every Sturm-Liouville problem, we can find a set of eigenfunctions which spans the entire solution space. Mathematically, it can be written as

(87)¶\[y(x) = \sum_{n=1}^{\infty}c_n \varphi(x)\]

If the coefficient, $c_n$, can be properly chosen and make this series converges to $y(x)$. Then it’s called eigen function expansion. The problem is how to determine a proper set of coefficient. Here, we gonna leverage one important characteristic of eigen function in Sturm-Liouville problem: weighted orthogonality. It describes that the weighted inner product of eigenfunctions which share different eigen values equals 0. i.e.,

(88)¶\[\int_{a}^{b}p(x)\varphi (x)\psi(x)dx= 0\]

Proof of Weighted Orthogonality of Eigenfunctions

Proof:

\[\int_{a}^{b}p(x)\varphi (x)\psi(x)dx= 0; \; x \in [a,b]\]

we know that

\[\begin{split}\begin{align} & (r\varphi^{'})^{'}+(q+\lambda p)\varphi = 0 \\ & (r\psi^{'})^{'}+(q+\mu p)\psi = 0 \\ \end{align}\end{split}\]

if we multiply the first equation by $\psi$ and the second equation by $\varphi$ and take the difference between two, we have

\[(r\varphi^{'})^{'}\psi-(r\psi^{'})^{'}\varphi+(\lambda-\mu)p(x)\varphi\psi = 0\]

or

\[\begin{split}\begin{align} &(r\varphi^{'}\psi)^{'}-r\varphi^{'}\psi^{'}-((r\psi^{'}\varphi)^{'}-r\varphi^{'}\psi^{'})+(\lambda-\mu)p(x)\varphi\psi \\ & = (r\varphi^{'}\psi)^{'}-(r\psi^{'}\varphi)^{'} +(\lambda-\mu)p(x)\varphi\psi \\ & = 0 \end{align}\end{split}\]

We also have the Wronskian of $\varphi$ and $\psi$

\[\begin{split}W[\varphi,\psi](x) = \begin{vmatrix} \varphi & \psi \\ \varphi^{'} & \psi^{'} \end{vmatrix} = \varphi\psi^{'}-\psi\varphi^{'}\end{split}\]

By observing the last equation above, one can find the second last equation can written as

\[(rW[\varphi,\psi](x))^{'}+(\lambda-\mu)p(x)\varphi\psi = 0\]

Geometrically, we know the Wronskian represents the area spanned by two solutions (or vector). If the two solutions are orthogonal, it further indicates

\[\int_{a}^{b}(\lambda-\mu)p(x)\varphi\psi = 0\]

while the two solution share different eigen values. The equation implies

\[\int_{a}^{b}p(x)\varphi\psi dx= 0\]

The equation above is so-called weighted orthogonality, where $p(x)$ is the weighting or the stretch of coordinate. (i.e., the space of coordinate can be inhomogeneous)

We have proofed the weighted orthogonality and now we can go a step further showing how to find a proper set of coefficient for each eigen function

Finding Coefficients for Eigenfunctions

We know

\[f(x)=\sum_{k=1}^{\infty} c_k \varphi_k(x)\]

if we multiply the entire equation by $p(x)\varphi_n(x)$ and integrate over the domain of interest

\[\int_{a}^{b} p(x)f(x)\varphi_n(x)dx=\int_{a}^{b}\sum_{k=1}^{\infty} c_k p(x)\varphi_k(x)\varphi_n(x)dx\]

According to weighted orthogonality, $\varphi_k(x)\varphi_n(x)$ is 0 as long as $k\neq n$. This leads to

\[\int_{a}^{b} p(x)f(x)\varphi_n(x)dx=\int_{a}^{b} c_k p(x)\varphi^{2}_n(x)dx\]

Reorganize the equation, we can find,

\[\frac{\int_{a}^{b} p(x)f(x)\varphi_n(x)dx}{\int_{a}^{b} p(x)\varphi^{2}_n(x)dx}= c_k \]

Although the equation above looks complicated, it’s simply the weighted covariance of $f(x)$ and $\varphi_n(x)$ divided by the weighted variance of $\varphi_n(x)$.

Example 3

Solve

\[\begin{split}\begin{align} & y^{''}+\lambda y=f(x); \; y^{'}(0)=y^{'}(2\pi)=0 \\ & f(t) = \begin{cases} x & \text{if $0\leq x<2$} \\ 6 & \text{if $2 \leq t \leq 2\pi$} \end{cases} \end{align}\end{split}\]

From example 2, we know the homogeneous solution is

\[y(x) = a\cos(\frac{n}{2}x)+b\sin(\frac{n}{2}x)\]

Given the boundary conditions, we know

\[y(x) = a\cos(\frac{n}{2}x);\; \textrm{where $\lambda=\frac{n^2}{4}$ and $n\in 0,1,2,3...$} \]

or we can written the solution as the linear combinations of different eigen function

\[y(x) = \sum_{n=0}^{\infty}c_n \cos(\frac{n}{2}x) \]

Using the concept of variation of parameters, we would like to find a proper set of $c_n$, which can match the inhomogeneous case.

For $n=0$ case,

\[c_0 = \frac{\int_{0}^{2\pi} f(x) \cos(\frac{n}{2}x) dx}{\int_{0}^{2\pi}\cos(\frac{n}{2}x)^2 dx}|_{n=0} = \frac{\frac{1}{2}x^2|^{x=2}_{x=0}+6x|^{x=2\pi}_{x=2}}{2\pi}=6-\frac{5}{\pi}\]

For $n=1$ and higher cases,

\[\begin{split}\begin{align} c_n &= \frac{\int_{0}^{2\pi} f(x) \cos(\frac{n}{2}x) dx}{\int_{0}^{2\pi}\cos(\frac{n}{2}x)^2 dx} \\ &= \frac{\int_{0}^{2}x\cos(\frac{n}{2}x)dx +\int_{2}^{2\pi}6\cos(\frac{n}{2}x)dx}{\int_{0}^{2\pi} \cos(\frac{n}{2}x)^2 dx} \\ &= \frac{\frac{2}{n^2}(\frac{n}{2}\sin(\frac{n}{2}x)x+\cos(\frac{n}{2}x))|_{x=0}^{x=2}+\frac{12}{n}\sin(\frac{n}{2}x)|^{x=2\pi}_{x=2}}{\int_{0}^{2\pi} \cos(nx)+\frac{1}{2} dx} \\ &= \frac{4(\cos(n)-1+n\sin(n))}{n^2\pi}+\frac{12\sin(n)}{n\pi} \end{align}\end{split}\]

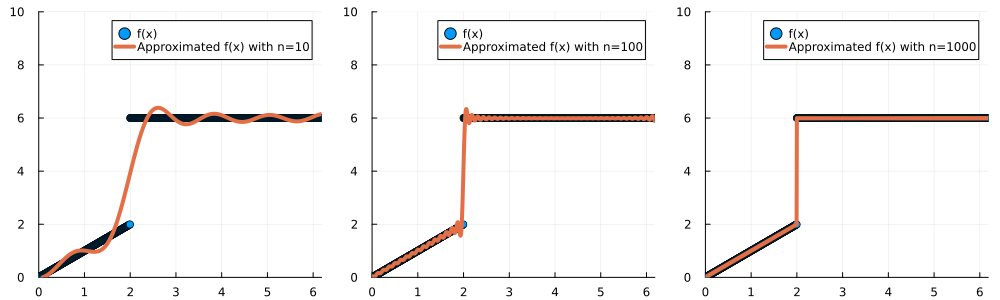
Fig. 8 An visualization of solutions with $n=10$, $n=100$, and $n=1000$¶

The code below (based on Julia) shows how to implement eigenfunction expansions in an ODE problem practically.

using Plots
x  = range(0, 2π, length=1000)
y1 = range(0, 2π, length=1000) 
y2 = one.(x)*6                 
f  = zero.(x)
f[ 0 .<= x .< 2]  = y1[ 0 .<= x .< 2]     # jump condition, when 0<=x<2,   f(x)=x 
f[ 2 .<= x .<= 2π]= y2[ 2 .<= x .<= 2π]   # jump condition, when 2<=x<2pi, f(x)=6

approx_y = reshape(zero.(x),1, length(x))
for n  in 0:10
    f    = reshape(f, 1, length(x))          # function f
    y4   = reshape(cos.(n/2*x),1, length(x))  # cos basis
    coef = y4*transpose(f)/(y4*transpose(y4)) # calculate the coefficient for each cos function 
    approx_y = approx_y+coef*y4               
end
p1 = scatter(x,y3,xlims=(0,2π),ylims=(0,10),width=2,label="f(x)")
plot!(reshape(x,length(x),1),reshape(approx_y,length(x),1),xlims=(0,2π),ylims=(0,10),label="Approximated f(x) with n=10",width=4)

Fourier Analysis¶

Boundary Conditions and Types of Solutions¶

In this section, we will introduce the famous Fourier Series to the reader. The Fourier analysis or Fourier Series is, however, nothing new than what we learned previously. Indeed, Fourier series is a special type of Sturm-Liouville problem, where $r(x)=1$, $q(x)=0$, and $r(x)=1$. In addition, it is usually given with a periodic boundary conditions. Physically, the readers can picture this type of Sturm-Liouville problem has a wave-like solution, where higher higher eigen values correspond to higher wave numbers. We will provide a more strict definition about the existence of Fourier Solutions (i.e., if the solutions can converge) at the chapter of Partial Differential Equations.

According to the types of boundary conditions, we can decide whether the solution is a Fourier sin function, cos function, or the combination of both.

Boundary Conditions for Fourier sin/cos and both series

In a Sturm-Liouville form, if the function is bounded (i.e., $\in [a,b]$), we can tell the types of Fourier solutions based on the boundary conditions

For Fourier $\sin$ series, we usually have boundary conditions $y(a)=0$ and $y(b)=0$
For Fourier $\cos$ series, we usually have boundary conditions $y^{'}(a)=0$ and $y^{'}(b)=0$
For the combinations of both $\sin$ and $\cos$, we have boundary conditions $a_1y(a)+a_2y^{'}(a)=0$ and $b_1y(b)+b_2y^{'}(b)=0$, or $y(a)=y(b)$ and $y^{'}(a)=y^{'}(b)$

One can easily find that they correspond to types I and II boundary conditions. An easy way to memorize the three boundary conditions is to find their connections with $\cos$ and $\sin$ functions. If we want a solution where the boundary is 0, then it can only be a $\sin$ function since $\cos(0)=1$. Similarly, if we want a function, which always has $0$ derivative (flat) at the boundary, then it can only be a $\cos$ function since $\sin$ function has the maximum/minimum derivative at $\frac{d \sin(x=0)}{dx}=1$.

Let’s have some practices and guess the solutions for the following ODEs.

Example 4

Find the solutions for the following ODE

\[y^{''}+\lambda y = f(x); \; y(-L)=y(L),\;y^{'}(-L)=y^{'}(L)\]

From the discussion above, we know this is a periodic boundary. Therefore, the solutions can be written as

(89)¶\[\begin{split}\begin{align} y&=\sum_{n=0}^{\infty} a_n\cos(\frac{2\pi n x}{(L-(-L))})+b_n\sin(\frac{2\pi n x}{(L-(-L))}) \\ &= \sum_{n=0}^{\infty} a_n\cos(\frac{n\pi x}{L})+b_n\sin(\frac{n\pi x}{L}) \end{align}\end{split}\]

where $2\pi$ and $2L$ indicates that the longest wave we can resolve is the wave that complete one cycle (one period) from the left end to the right end of the domain. Now, following the eigenfunction expansion, we can determine the coefficient for different $n$.

(90)¶\[\begin{split}\begin{align} a_n & = \frac{\int_{-L}^{L}f(x)\cos(\frac{n\pi x}{L})dx}{\int_{-L}^{L}\cos(\frac{n\pi x}{L})^2dx} \\ b_n & = \frac{\int_{-L}^{L}f(x)\sin(\frac{n\pi x}{L})dx}{\int_{-L}^{L}\sin(\frac{n\pi x}{L})^2dx} \\ \end{align}\end{split}\]

The equation above is so-called discrete Fourier Transform, where we convert $f(x)$ from the physical space to frequency (wave number) space. If we can make the summation form into a integral form (making discrete function into a continuous function) by assuming (1) $k = \frac{n\pi}{L}$ and (2) domain of integral $[-\infty,\infty]$. (Let readers to walk through the derivation) Then, we will have

(91)¶\[y=\int_{0}^{\infty} a_k\cos(kx)+b_k\sin(kx)dk\]

, which is the Fourier integral. Following the same approach of finding Fourier coefficients,

(92)¶\[\begin{split}\begin{align} a_k & = \frac{\int_{-\infty}^{\infty}f(x)\cos(kx)dx}{\int_{-\infty}^{\infty}\cos(kx)^2dx} \\ b_k & = \frac{\int_{-\infty}^{\infty}f(x)\sin(kx)dx}{\int_{-\infty}^{\infty}\sin(kx)^2dx} \\ \end{align}\end{split}\]

Power Spectrum, Windows and Gibbs Phenomenon¶

From the Fourier Transform above, the readers can find that we can determine the precision of accuracy by truncating the solutions. For example, in Fig. 8, the approximated solution is nearly identical to $f(x)$ when $n$ goes to 1000. It also indicates that we can filter out the small feature in the solution by heavily truncating the solutions. To know what kind of signals is retained, we can apply power spectrum analysis to a given $f(x)$,

The power spectrum of a given wave number of defined as

(93)¶\[\textrm{variance explained} = \frac{a_k^2+b_k^2}{2} (= \frac{c_k^2}{2})\]

(93) evidently has an energy form (squared form) given that we want know the amplitude of a given wave number instead of its sign. It is equivalent to the explained variance of $f(x)$ by certain wave number like what we learn in linear regression. If one looks closely to (89) and (90), Fourier Transform is indeed a linear regression problem where different types of waves are our predictors and both $a_n$ and $b_n$ are the corresponding regression coefficients.

Recall that the Convolution in Laplace transform has similar effect. Where we can apply a Heaviside function with 2 jump conditions to filter out the high frequency signals that we don’t want. However, Fourier Transform is a more strict way of filtering data. To demonstrate that, we can apply Fourier transform to a Heaviside function with 2 jump conditions.

The Fourier Transform of a Heaviside function

Given a Heaviside function,

\[\begin{split}g(t)=H(t-0)-H(t-1) = \begin{cases} 0 & \text{if $t<-\frac{T}{2}$} \\ 1 & \text{if $t>=-\frac{T}{2}$ and $t<\frac{T}{2}$} \\ 0 & \text{if $t>=\frac{T}{2}$ } \end{cases}\end{split}\]

take the Fourier transform of function $g(x)$, we have

\[\begin{split}\begin{align} a_k &= \frac{\int^{\infty}_{-\infty} g(x)\cos(kx)dx}{\int^{\infty}_{-\infty} \cos(kx)^2 dx}=\frac{\int^{\frac{T}{2}}_{-\frac{T}{2}} \cos(kx)dx}{\int^{\pi}_{-\pi} \cos(kx)^2 dx} = \frac{1}{k\pi}\sin(kx)|^{x=\frac{T}{2}}_{x=-\frac{T}{2}}= \frac{2}{\pi}\textrm{sinc(kT/2)}\\ b_k &= \frac{\int^{\infty}_{-\infty} g(x)\sin(kx)dx}{\int^{\infty}_{-\infty} \sin(kx)^2 dx}=\frac{\int^{\frac{T}{2}}_{-\frac{T}{2}} \sin(kx)dx}{\int^{\pi}_{-\pi} \sin(kx)^2 dx} = -\frac{1}{k\pi}\cos(kx)|^{x=\frac{T}{2}}_{x=-\frac{T}{2}} = 0 \end{align}\end{split}\]

One can find we have a $\textrm{sinc}(\frac{kT}{2})$ function. The figure below shows how does it look like on a power spectrum.

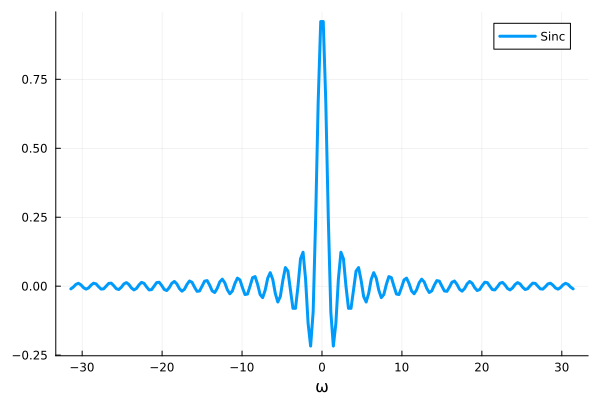
Fig. 9 An visualization of sinc function centers around the specified wave number (we shift it to 0).¶

One can find that the signal not only centers around the wave number of interest but also spreads out to its neighbor. This indicates when we use a Heaviside function for filtering, we can’t entirely remove the signal outside the wave numbers of interest. This is the famous Principle of Uncertainty, where the wiggles on the edge are so-called Gibbs Phenomenon. This is similar to Principle of Uncertainty in quantum physics where the momentum (in frequency space) is the Fourier transform of the wave function’s location.

Applied Math 2

Week 7 and 8: Sturm-Liouville Theorem: Eigenfunctions and Fourier Series

Contents